通过随机询问110名性别不同的行人，对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查，得到如下的列联表：
| |
男 |
女 |
总计 |
| 走天桥 |
40 |
20 |
|
| 走斑马线 |
20 |
30 |
|
| 总计 |
|
|
|
（
）
 |
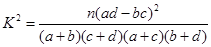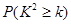0.050 0.010 0.001 |
 |
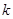3.841 6.635 10.828 |
（1）完成表格
（2）能否在犯错误的概率不超过0.010的前提下认为性别与愿意走斑马线还是愿意走人行天桥有关系。
为何值时，直线
．
；（2）在
轴上的截距为１．
，直线
，求：
且与
平行的直线的方程；
，
，
求直线
，
，
的斜率，并判断这些直线的倾斜角是锐角还是钝角．
，
，
，
为顶点的四边形的形状，并说明理由．
与
．