阅读下列材料:
我们知道,一次函数y=kx+b的图象是一条直线,而y=kx+b经过恒等变形可化为直线的另一种表达形式:Ax+Bx+C=0(A、B、C是常数,且A、B不同时为0).如图1,点P(m,n)到直线l:Ax+Bx+C=0的距离(d)计算公式是:d= .
.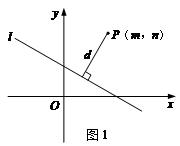
例:求点P(1,2)到直线y=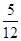 x-
x- 的距离d时,先将y=
的距离d时,先将y=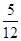 x-
x- 化为5x-12y-2=0,再由上述距离公式求得d=
化为5x-12y-2=0,再由上述距离公式求得d= =
= .
.
解答下列问题:
如图2,已知直线y=-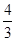 x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).
x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).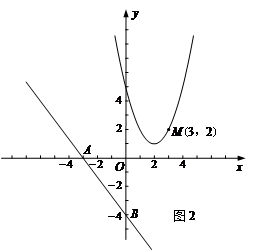
(1)求点M到直线AB的距离.
(2)抛物线上是否存在点P,使得△PAB的面积最小?若存在,求出点P的坐标及△PAB面积的最小值;若不存在,请说明理由.
把一副三角板如图甲放置,其中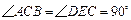 ,
, ,
, ,斜边
,斜边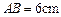 ,
,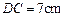 。把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙)。这时AB与CD1相交于点
。把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙)。这时AB与CD1相交于点 ,与D1E1相交于点F。
,与D1E1相交于点F。求
 的度数;
的度数;求线段AD1的长;
若把三角形D1CE1绕着点
 顺时针再旋转30°得△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?说明理由。
顺时针再旋转30°得△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?说明理由。

如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,图中的三个扇形(即三个阴影部分)的面积之和是多少?弧长的和为多少?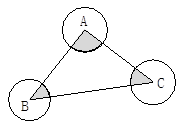
先阅读,再解答:
我们在判断点 是否在直线
是否在直线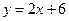 上时,常用的方法:把
上时,常用的方法:把 代入
代入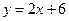 中,由
中,由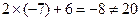 ,判断出点
,判断出点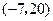 不在直线
不在直线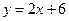 上。小明由此方法并根据“两点确定一条直线”,推断出点A(1,2),B(3,4),C(-1,6)三点可以确定一个圆。你认为他的推断正确吗?请你利用上述方法说明理由。
上。小明由此方法并根据“两点确定一条直线”,推断出点A(1,2),B(3,4),C(-1,6)三点可以确定一个圆。你认为他的推断正确吗?请你利用上述方法说明理由。
解方程: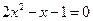 。
。
在如图所示的2004年1月份日历中,
| 星期日 |
星期一 |
星期二 |
星期三 |
星期四 |
星期五 |
星期六 |
| 1 |
2 |
3 |
||||
| 4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 11 |
12 |
13 |
14 |
15 |
16 |
17 |
| 18 |
19 |
20 |
21 |
22 |
23 |
24 |
| 25 |
26 |
27 |
28 |
29 |
30 |
31 |
用一个长方形的方框圈出任意3×3个数.如果从左下角到右上角的“对角线”上的3个数字的和为45,那么这9个数的和为,在这9个日期中,最后一天是号;
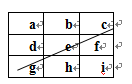
用一个长方形方框圈出任意2×2个数(如4,5,11,12),你能发现这四个数有怎样的关系?请用一个等式表示a,b,c,d 之间的关系.