袋中装有除数字不同其它都相同的六个小球,球上分别标有数字1,2,3,4,5,6.
(1)从袋中摸出一个小球,求小球上数字小于3的概率;
(2)将标有1,2,3数字的小球取出放入另外一个袋中,分别从两袋中各摸出一个小球,
求数字之和为偶数的概率.(要求用列表法或画树状图求解)
我们知道三角形三条中线的交点叫做三角形的重心.经过证明我们可得三角形重心具备下面的性质: 重心到顶点的距离与重心到该顶点对边中点的距离之比为2﹕1.请你用此性质解决下面的问题.
已知:如图,点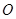 为等腰直角三角形
为等腰直角三角形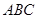 的重心,
的重心,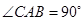 ,直线
,直线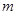 过点
过点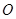 ,过
,过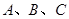 三点分别作直线
三点分别作直线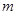 的垂线,垂足分别为点
的垂线,垂足分别为点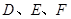 .
.
<1>当直线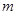 与
与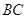 平行时(图1),请你猜想线段
平行时(图1),请你猜想线段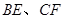 和
和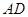 三者之间的数量关系并证明;
三者之间的数量关系并证明;
<2>当直线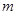 绕点
绕点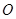 旋转到与
旋转到与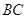 不平行时,分别探究在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段
不平行时,分别探究在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段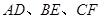 三者之间又有怎样的数量关系?请写出你的结论,不需证明.
三者之间又有怎样的数量关系?请写出你的结论,不需证明.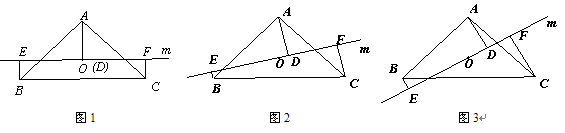
已知: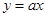 与
与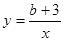 两个函数图象交点为
两个函数图象交点为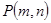 ,且
,且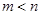 ,
,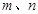 是关于
是关于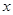 的一元二次方程
的一元二次方程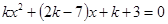 的两个不等实根,其中
的两个不等实根,其中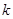 为非负整数.
为非负整数.<1>求
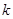 的值;
的值;<2>求
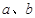 的值;
的值;<3>如果直线
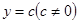 与函数
与函数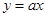 和
和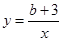 分别交于
分别交于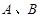 两点(点
两点(点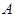 在点
在点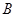 的左侧),线段
的左侧),线段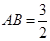 ,求
,求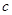 的值.
的值.
、在边长为1的正方形网格中,正方形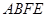 与正方形
与正方形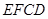 的位置如图所示.
的位置如图所示.
(1)请你按下列要求画图:
①联结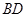 交
交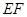 于点
于点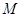 ;
;
②在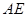 上取一点
上取一点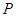 ,联结
,联结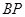 ,
,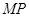 ,使△
,使△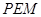 与△
与△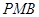 相似;
相似;(2)若
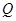 是线段
是线段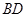 上一点,连结
上一点,连结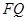 并延长交四边形
并延长交四边形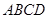 的一边于点
的一边于点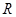 ,且满足
,且满足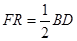 ,则
,则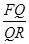 的值为_____________.
的值为_____________.
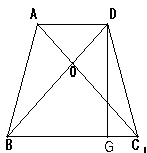
如图,在等腰梯形ABCD中,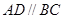 ,
,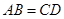 ,
,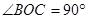 ,
,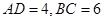
 |
<1>过D作
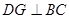 于G,则DG为梯形的高,求这个高DG;
于G,则DG为梯形的高,求这个高DG;<2>求
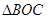 的面积。
的面积。
已知:抛物线C1: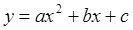 经过点
经过点 、
、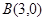 、
、
<1>求抛物线C1的解析式;
<2>将抛物线C1向左平移几个单位长度,可使所得的抛物线C2经过坐标原点,计算并写出C2的解析式;
<3>把抛物线C1绕点A(-1,O)旋转180o,直接写出所得抛物线C3顶点D的坐标.