1772年,法籍意大利数学家拉格朗日推断出:两个质量相差悬殊的天体(如太阳和地球)所在同一平面上有5个点,如图中的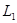 、
、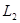 、
、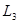 、
、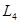 、
、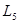 ,人们称为拉格朗日点,由于这五个点特殊性,已经成为各个航天大国深空探测所争夺的地方。2012年8月25日23时27分,经过77天的飞行,“嫦娥二号”在世界上首次实现从月球轨道出发,受控准确进入距离地球约150万公里远的太阳与地球引力平衡点拉格朗日
,人们称为拉格朗日点,由于这五个点特殊性,已经成为各个航天大国深空探测所争夺的地方。2012年8月25日23时27分,经过77天的飞行,“嫦娥二号”在世界上首次实现从月球轨道出发,受控准确进入距离地球约150万公里远的太阳与地球引力平衡点拉格朗日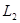 点的环绕轨道。拉格朗日
点的环绕轨道。拉格朗日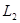 点位于太阳和地球连线的延长线上,“嫦娥二号”位于该点,在几乎不消耗燃料的情况下与地球同步绕太阳做圆周运动,下列说法正确的是
点位于太阳和地球连线的延长线上,“嫦娥二号”位于该点,在几乎不消耗燃料的情况下与地球同步绕太阳做圆周运动,下列说法正确的是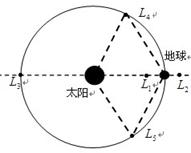
| A.“嫦娥二号”绕太阳运动周期和地球绕太阳运动周期相等 |
| B.“嫦娥二号”在该点处于平衡状态 |
| C.“嫦娥二号”所需向心力不可能仅由太阳的引力提供 |
| D.“嫦娥二号”的绕太阳运动的向心加速度大于地球绕太阳运动的向心加速度 |
如图7,在半径为R的圆内有一磁感应强度为B的向外的匀强磁场,一质量为m,电量为q的粒子(不计重力),从A点对着圆心方向垂直射入磁场,从C点飞出,则()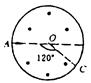
| A.粒子带负电 | B.粒子的轨道半径为R |
C.A、C二点相距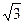 R R |
D.粒子在磁场中运动的时间为2πm/3Bq |
如图所示,半圆形光滑槽固定在地面上,匀强磁场与槽面垂直。将质量为m的带电小球自槽口A处由静止释放,小球到达槽最低点C处时,恰好对槽无压力,则小球在以后的运动过程中对C的最大压力为()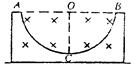
| A.0 | B.2mg | C.4mg | D.6mg |
两个粒子,带电量相等,在同一匀强磁场中只受磁场力而作匀速圆周运动.()
| A.若速率相等,则半径必相等 | B.若质量相等,则周期必相等 |
| C.若动量大小相等,则半径必相等 | D.若动能相等,则周期必相等 |
如图所示,每个电子都绕着同样的正电荷做匀速圆周运动,轨道半径相等,在(a)、(b)情况下,轨道平面与匀强磁场B垂直.设三种情况下电子转动的角速度分别为ωa、ωb、ωc,则: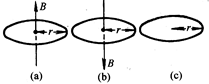
| A.ωa>ωc>ωb | B.ωa>ωb>ωc | C.ωa=ωb=ωc | D.ωa<ωc<ωb |
图为万用表欧姆挡的原理示意图,其中电流表的满偏电流为300μA,内阻 rg=100Ω,调零电阻最大阻值R=50kΩ,串联的固定电阻R0=50Ω,电池电动势
ε=1.5V.用它测量电阻Rx,能准确测量的阻值范围是:()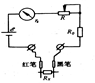
| A.30kΩ~80kΩ |
| B.3kΩ~8kΩ |
| C.300Ω~800Ω |
| D.30Ω~80Ω |