某同学设计了一个研究平抛运动的实验装置,如图,在水平桌面上放置一个斜面,让钢球从斜面上由静止滚下,钢球滚过桌边后做平抛运动。在钢球抛出后经过的地方放置一块水平木板,木板由支架固定成水平,木板所在高度可通过竖直标尺读出,木板可以上下自由调节。在木板上固定一张白纸。该同学在完成装置安装后进行了如下步骤的操作: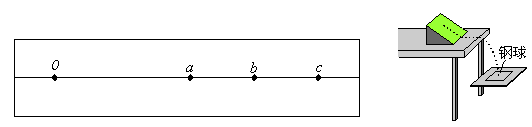
A.实验前在白纸上画一条直线,并在线上标出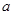 、 、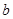 、 、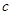 三点,且 三点,且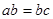 ,如图所示,量出 ,如图所示,量出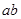 长度 长度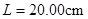 。 。 |
B.让钢球从斜面上的某一位置由静止滚下,调节木板高度,使得钢球正好击中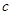 点,记下此时木板离地面的高度 点,记下此时木板离地面的高度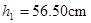 。 。 |
C.让钢球从斜面上的同一位置由静止滚下,调节木板高度,使得钢球正好击中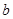 点,记下此时木板离地面的高度 点,记下此时木板离地面的高度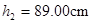 。 。 |
D.让钢球从斜面上的同一位置由静止滚下,调节木板高度,使得钢球正好击中a点,记下此时木板离地面的高度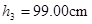 。重力加速度为 。重力加速度为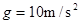 ,空气阻力不计。该同学由上述测量结果即可粗测出钢球的平抛初速度大小 ,空气阻力不计。该同学由上述测量结果即可粗测出钢球的平抛初速度大小 ,钢球击中 ,钢球击中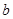 点时其竖直分速度大小为 点时其竖直分速度大小为 (结果均保留三位有效数字). (结果均保留三位有效数字). |
电源电动势E约为9 V,内阻r约为40 Ω,最大额定电流为50 mA。现有量程为0~3 V、内阻为2 kΩ的电压表V和阻值为0~999.9 Ω的电阻箱R各一只,另有若干定值电阻、开关和导线等器材。为测定该电源的电动势和内阻,某同学设计了如图所示的电路进行实验,请回答下列问题: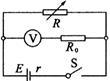

(1)实验室备有以下几种规格的定值电阻R0,实验中应选用的定值电阻是 。(填字母代号)
A.200Ω B.2 kΩ C.4 kΩ D.10 kΩ
(2)该同学接入符合要求的R0后,闭合开关S,调整电阻箱的阻值,读取电压表的示数。根据记录的多组数据,作出如图所示的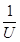 -
-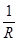 图线。根据该图线可求得电源的电动势E= V,内阻r = Ω.(保留两位有效数字)
图线。根据该图线可求得电源的电动势E= V,内阻r = Ω.(保留两位有效数字)
某实验小组欲以图甲装置中的小车(含固定在小车上的挡光片)为研究对象来验证“动能定理”.他们用不可伸长的细线将小车通过一个定滑轮与砝码盘相连,在水平桌面上的A、B两点各安装一个光电门,记录小车通过A、B时的遮光时间.若小车质量为M,砝码盘和盘中砝码的总质量为m.
(1)实验中,小车所受摩擦力的功不便测量,故应设法消除摩擦力对小车运动的影响,需要进行的操作是__________;
(2)在完成了(1)的操作后,为确保小车运动中受到的合力与砝码盘和盘中砝码的总重力大致相等,m、M应满足关系是__________.
(3)用游标卡尺测量挡光片的宽度d如图乙所示,则d =__________mm;用刻度尺量得A、B之间的距离为L;
(4)将小车停在桌面上的C点,在砝码盘中放上砝码,小车在细线拉动下运动,小车通过A、B时的遮光时间分别为t1、t2,已知重力加速度为g,则本实验最终要探究的数学表达式应该是__________(用相应的字母m、M、t1、t2、L、d表示).
小明利用如图甲所示的电路测定旧电池组的电动势与内电阻。
⑴用笔画线代替导线将图乙中的实物连线补充完整;
⑵由图丙可知:该电池组的电动势E= V,内阻r=  (保留两位有效数字);
(保留两位有效数字);
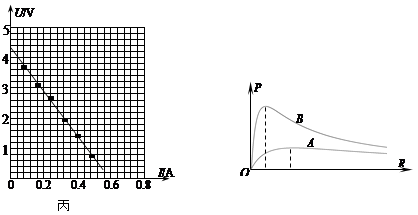
⑶小明又利用上述实验方案测定了同规格新电池组的电动势与内电阻。通过实验发现旧电池组与新电池组相比,电动势几乎没有变化,但它们的输出功率P随外电阻R变化的关系图线有较大差异,如图丁所示。可知图线 (选填“A”或“B”)对应的是新电池组,试说出判断的理由: 。
要测绘额定电压为2V的日常用小电珠的伏安特性曲线,所供选择的器材除了导线和开关外,还有以下一些器材可供选择:
| A.电源E(电动势3.0V,内阻可不计) |
| B.电压表V1(量程为0~3.0V,内阻约2kΩ) |
| C.电压表V2(0~15.0V,内阻约6kΩ |
| D.电流表A1(0~0.6A,内阻约1Ω) |
E.电流表A2(0~100mA,内阻约2Ω)
F.滑动变阻器R1(最大值10Ω)
G.滑动变阻器R2(最大值2kΩ)
(1)为减少实验误差,实验中电压表应选择__________,电流表应选择__________,滑动变阻器应选择__________(填各器材的序号)
(2)为提高实验精度,请你在如图a中设计实验电路图


(3)根据图a,在图b中把缺少的导线补全,连接成实验的电路.
(4)实验中移动滑动变阻器滑片,得到了小灯泡的U﹣I图象如图c所示,则该小电珠的额定功率是 w,小电珠电阻的变化特点是 .
在测定一节干电池的电动势和内电阻的实验中,备有下列器材: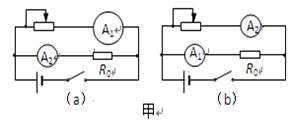
A.待测的干电池(电动势约为1.5 V,内电阻小于1.0 Ω )
B.电流表A1(量程0—3 mA,内阻 =10 Ω)
=10 Ω)
C.电流表A2(量程0—0.6 A,内阻 =0.1 Ω)
=0.1 Ω)
D.滑动变阻器R1(0—20 Ω,10 A)
E.滑动变阻器R2(0—200 Ω,l A)
F.定值电阻R0(990 Ω)
G.开关和导线若干
(1)某同学发现上述器材中虽然没有电压表,但给出了两个电流表,于是他设计了如图甲所示的(a)、(b)两个参考实验电路,其中合理的是______图所示的电路;在该电路中,为了操作方便且能准确地进行测量,滑动变阻器应选______(填写器材前的字母代号)。
(2)图乙为该同学根据(1)中选出的合理的实验电路,利用测出的数据绘出的I1-I2图线(I1为电流表A1的示数,I2为电流表A2的示数,且I2的数值远大于I1的数值),则由图线可得被测电池的电动势E=____________V,内阻r=____________Ω。(结果保留小数点后2位)
(3)若将图线的纵坐标改为_______________,则图线与纵坐标轴的交点的物理含义即为电动势的大小。