如图所示，半径为R的光滑半圆环轨道竖直固定在一水平光滑的桌面上，桌面距水平地面的高度也为R，在桌面上轻质弹簧被a、b两个小球挤压（小球与弹簧不拴接），处于静止状态．同时释放两个小球，小球a、b与弹簧在水平桌面上分离后，a球从B点滑上光滑半圆环轨道并恰能通过半圆环轨道最高点A，b球则从桌面C点滑出后落到水平地面上，落地点距桌子右侧的水平距离为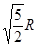
．已知小球a质量为m，重力加速度为g．求：
（1）释放后b球离开弹簧时的速度大小．
（2）释放后a球离开弹簧时的速度大小．
（3）小球b的质量.
（4）释放小球前弹簧具有的弹性势能．
如图，实线是某时刻的波形曲线，虚线是0.2S后的波形曲线，这列波的最大周期和最小波速是多少？若波速是35m/s，则这列波的传播方向如何？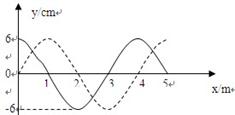
某研究性学习小组首先根据小孔成像原理估测太阳半径，再利用万有引力定律估算太阳的密度.准备的器材有:①不透光圆筒，一端封上不透光的厚纸，其中心扎一小孔，另一端封上透光的薄纸；②毫米刻度尺.已知地球绕太阳公转的周期为T，万有引力常量为G.要求:(1)简述根据小孔成像原理估测太阳半径R的过程.(2)利用万有引力定律推算太阳密度.
如图所示，两根足够长的直金属导轨MN、PQ平行放置在倾角为θ的绝缘斜面上，两导轨间距为L。M、P两点间接有阻值为R的电阻。一根质量为m的均匀直金属杆ab放在两导轨上，并与导轨垂直。整套装置处于匀强磁场中，磁场方向垂直于斜面向上。导轨和金属杆的电阻可忽略。让金属杆ab沿导轨由静止开始下滑，经过足够长的时间后，金属杆达到最大速度vm，在这个过程中，电阻R上产生的热为Q。导轨和金属杆接触良好，它们之间的动摩擦因数为μ，且μ<tanθ。已知重力加速度为g。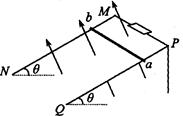
(1)求磁感应强度的大小；
(2)金属杆在加速下滑过程中，当速度达到
时，求此时杆的加速度大小；
(3)求金属杆从静止开始至达到最大速度的过程中下降的高度。
发电站通过升压变压器、输电导线和降压变压器把电能输送到用户,如果升压变压器和降压变压器都可视为理想变压器。如图所示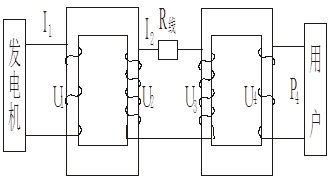
(1)若发电机的输出功率是 100 kW,输出电压是250 V,升压变压器的原、副线圈的匝数比为 1∶25,求升压变压器的输出电压和输电导线中的电流；
(2)若输电导线中的电功率损失为输入功率的 4%,求输电导线的总电阻和降压变压器原线圈两端的电压。
如图所示，放置在水平面内的平行金属框架宽为L=0.4m，金属棒ab置于框架上，并与两框架垂直，整个框架位于竖直向下、磁感强度B=0.5T的匀强磁场中，电阻R=0.09Ω，ab的电阻r=0.01Ω，摩擦不计，当ab在水平恒力F作用下以v=2.5m/s的速度向右匀速运动时，求: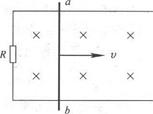
(1) 回路中的感应电流的大小；
(2) 恒力F的大小；
(3) 电阻R上消耗的电功率.