小华爸爸上星期五买进某公司股票1000股，每股27元，下表为本周内每日该股票的涨跌情况。（单位：元）
| 星期 |
一 |
二 |
三 |
四 |
五 |
| 每股涨跌 |
+4 |
-1 |
-2.5 |
+4.5 |
-6 |
（1）通过上表你认为星期三收盘时，每股是多少元？
（2）本周内每股最高是多少元？最低是多少元？
（3）已知小华爸爸买进股票时付了千分之3的手续费，卖出时因优惠免手续费但要交成交额千分之2的交易税，如果小华爸爸在星期五收盘前将全部股票卖出，他的收益情况如何？
(本小题满分6分)解不等式组
.
运用“同一图形的面积不同表示方式相同”可以证明一类含有线段的等式，这种解决问题的方法我们称之为面积法． 如图1，在等腰三角形ABC中，AB=AC，AC边上的高为
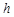，M是底边BC上的任意一点，点M到腰AB、AC的距离分别为
、
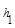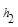．连接AM,可得结论
+
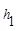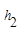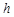=．当点M在BC延长线上时，
、
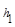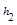、之间的等量关系式是．（直接写出结论不必证明）．
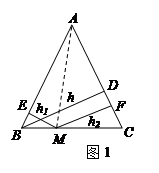
应用：平面直角坐标系中有两条直线
：
、
：
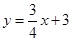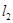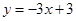，若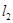上的一点M到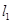的距离是1．请运用（1）的条件和结论求出点M的坐标．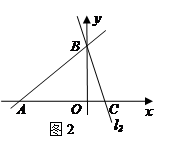
张老师于2010年9月份在杭州买了一套楼房，当时(即9月份)在建行贷款96万元，贷款期限为20年，从开始贷款的下一个月起逐月偿还，贷款月利率是0.5%(每月还款数额＝平均每月应还的贷款本金＋月利息，月利息＝上月所剩贷款本金数额×月利率)．求张老师借款后第一个月的还款数额．
假设贷款月利率不变，请写出张老师借款后第n(n是正整数)个月还款数额p与n之间的函数关系式(不必化简)．
在(2)的条件下，求张老师2011年10份的还款数额．
已知△ABC，∠ACB=90º，AC=BC，点E、F在AB上，∠ECF=45º，设△ABC的面积为S，说明AF·BE=2S的理由。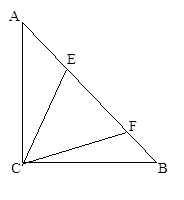
在萧山区第二届汽车展期间，某汽车经销商推出
四种型号的小轿车共1000辆进行展销．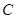
型号轿车销售的成交率为50%，其它型号轿车的销售情况绘制在图1和图2两幅尚不完整的统计图中．参加展销的
型号轿车有多少辆？请你将图2的统计图补充完整；
通过计算说明，哪一种型号的轿车销售情况最好？
