如图,在梯形纸片ABCD中,BC∥AD,∠A+∠D=90°,tanA=2,过点B作BH⊥AD与H,BC=BH=2.动点 从点
从点 出发,以每秒1个单位的速度沿
出发,以每秒1个单位的速度沿 运动到点
运动到点 停止,在运动过程中,过点
停止,在运动过程中,过点 作
作 交折线
交折线 于点
于点 ,将纸片沿直线
,将纸片沿直线 折叠,点
折叠,点 、
、 的对应点分别是点
的对应点分别是点 、
、 。设
。设 点运动的时间是
点运动的时间是 秒(
秒( )。
)。
(1)当点 和点
和点 重合时,求运动时间
重合时,求运动时间 的值;
的值;
(2)在整个运动过程中,设 或四边形
或四边形 与梯形
与梯形 重叠部分面积为
重叠部分面积为 ,请直接写出
,请直接写出 与
与 之间的函数关系式和相应自变量
之间的函数关系式和相应自变量 的取值范围;
的取值范围;
(3)平移线段 ,交线段
,交线段 于点
于点 ,交线段
,交线段 。在直线
。在直线 上存在点
上存在点 ,使
,使 为等腰直角三角形。请求出线段
为等腰直角三角形。请求出线段 的所有可能的长度。
的所有可能的长度。
邮递员骑车从邮局出发,先向北骑行2 km达到A村,继续向北骑行3 km达到B村,然后向南骑行9 km达到C村,最后回到邮局.
(1)以邮局为原点,向北方向为正方向,用1 cm表示1 km,画出数轴,并在数轴上表示A、B、C三个村庄的位置.
(2)C村离A村多远?
(3)邮递员一共骑行了多少km?
解答下列各题:
(1)先化简,再求值: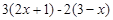 ,其中
,其中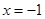 ;
;
(2)如果代数式5a+3b的值为-4,那么代数式-2(a+b)-4(2a+b)的值是多少?请写出你的解题过程.
公安人员在破案时常常根据案发现场作案人员留下的脚印推断犯人的身高.如果用a表示脚印长度,b表示身高.这两者之间的关系类似于b=7a—3.
(1)某人脚印长度为24cm,则他的身高约为多少?
(2)在某次案件中,抓获了两名可疑人员,一个身高为1.87m,另一个身高为1.65m,现场测量的脚印长度为27cm,请你帮助侦破一下,哪个可疑人员的作案可能性更大?
在数轴上把下列各数表示出来,并用“<”连接各数.
- ,
, ,
, ,-(-
,-(-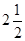 ),+
),+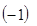 ,
, 22.
22.
把下列各数分别填入相应的集合里.
-1.8,0, ,0.1
,0.1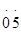 ,-
,-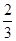 ,-1.4343343334…(每两个4之间1的个数逐次加1),
,-1.4343343334…(每两个4之间1的个数逐次加1),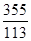 .
.
正数集合:(…);
负数集合:(…);
有理数集合:(…);
无理数集合:(…).