有4男3女共7位同学从前到后排成一列.
(1)有多少种不同方法?
(2)甲不站在排头,有多少种不同方法?
(3)三名女生互不相邻,有多少种不同方法?
(4)3名女生在队伍中按从前到后从高到矮顺序排列,有多少种不同方法?
(5)3名女生必须站在一起,有多少种不同方法?
已知等腰梯形PDCB中(如图),PB=3,DC=1,PD=BC=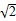 ,A为PB边上一点,且PA=1,将△PAD沿AD折起,使平面PAD⊥平面ABCD(如图).
,A为PB边上一点,且PA=1,将△PAD沿AD折起,使平面PAD⊥平面ABCD(如图).
(1)证明:平面PAD⊥平面PCD.
(2)试在棱PB上确定一点M,使截面AMC把几何体分成的两部分VPDCMA∶VMACB=2∶1.
(3)在M满足(2)的情况下,判断直线PD是否平行平面AMC.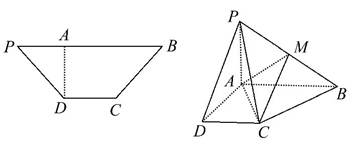
如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆O上的点.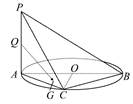
(1)求证:平面PAC⊥平面PBC.
(2)设Q为PA的中点,G为△AOC的重心,求证:QG∥平面PBC.
如图,AB=AD,∠BAD=90°,M,N,G分别是BD,BC,AB的中点,将等边△BCD沿BD折叠到△BC′D的位置,使得AD⊥C′B.
(1)求证:平面GNM∥平面ADC′.
(2)求证:C′A⊥平面ABD.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1,且E是BC中点.
(1)求证:A1B∥平面AEC1.
(2)求证:B1C⊥平面AEC1.
一个几何体是由圆柱ADD1A1和三棱锥E-ABC组合而成,点A,B,C在圆O的圆周上,其正(主)视图,侧(左)视图的面积分别为10和12,如图所示,其中EA⊥平面ABC,AB⊥AC,AB=AC.AE=2.
(1)求证:AC⊥BD.
(2)求三棱锥E-BCD的体积.