如图,已知∠AOB以O为圆心,以任意长为半径作弧,分别交OA、OB于F、E两点,再分别以E、F为圆心,大于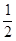 EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D。
EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D。
(1)若∠OFD=116°,求∠DOB的度数;
(2)若FM⊥OD,垂足为M,求证△FMO≌△FMD.
已知 ,求代数式
,求代数式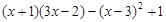 的值.
的值.
求不等式组 的整数解.
的整数解.
已知:如图,C为BE上一点, 点A、D分别在BE两侧,AB∥ED,∠ACB=∠CDE,BC=ED.求证:AC=CD.
如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.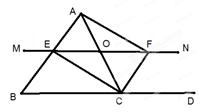
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论。
阅读下面的情景对话,然后解答问题:
(1)①根据“奇异三角形”的定义,小红得出命题:“等边三角形一定是奇异三角形”·请判断小红提出的命题是否正确,并填空 (填“正确”或“不正确”);
②若某三角形的三边长分别是2、4、 ,则
,则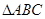 是奇异三角形吗? (填“是”或“不是”);
是奇异三角形吗? (填“是”或“不是”);
(2)在 中,
中, .AB=c,AC=b. BC=a,且b>a,若
.AB=c,AC=b. BC=a,且b>a,若 是奇异三角形.求a:b:c;
是奇异三角形.求a:b:c;
(3)如图, 中
中 ,以AB为斜边作等腰直角三角形ABD,点E是AC上方的一点,且满足AE=AD,CE=CB.
,以AB为斜边作等腰直角三角形ABD,点E是AC上方的一点,且满足AE=AD,CE=CB.
①求证:△ACE是奇异三角形;
②当△ACE是直角三角形时,求∠DBC的度数.