已知圆C: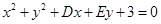 关于直线
关于直线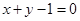 对称,圆心在第二象限,半径为
对称,圆心在第二象限,半径为
(1)求圆C的方程;
(2)是否存在斜率为2的直线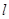 ,
,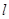 截圆C所得的弦为AB,且以AB为直径的圆过原点,若存在,则求出
截圆C所得的弦为AB,且以AB为直径的圆过原点,若存在,则求出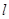 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
设 的内角
的内角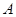 ,
, ,
,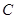 所对的边长分别为
所对的边长分别为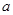 ,
,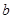 ,
,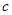 且
且 ,
,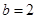 .
.
(1)若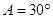 ,求
,求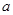 的值;
的值;
(2)若 的面积为3,求
的面积为3,求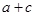 的值.
的值.
已知椭圆 的离心率为
的离心率为 ,椭圆的的一个顶点和两个焦点构成的三角形的面积为4.
,椭圆的的一个顶点和两个焦点构成的三角形的面积为4.
(1)求椭圆C的方程;
(2)已知直线 与椭圆C交于A, B两点,若点M(
与椭圆C交于A, B两点,若点M( ,0),求证
,0),求证 为定值.
为定值.
数列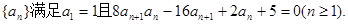 记
记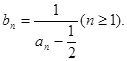
(1)求b1、b2、b3、b4的值;
(2)求数列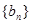 的通项公式及数列
的通项公式及数列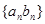 的前n项和
的前n项和
如图所示,四棱锥P—ABCD中,AB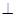 AD,CD
AD,CD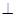 AD,PA
AD,PA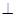 底面ABCD,PA=AD=CD=2AB=2,M为PC的中点.
底面ABCD,PA=AD=CD=2AB=2,M为PC的中点.
(1)求证:BM∥平面PAD;
(2)在侧面PAD内找一点N,使MN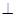 平面PBD;
平面PBD;
(3)求直线PC与平面PBD所成角的正弦.
在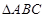 中,
中, 分别是角A,B,C的对边,且满足
分别是角A,B,C的对边,且满足 .
.
(1)求角B的大小;
(2)若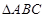 最大边的边长为
最大边的边长为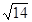 ,且
,且 ,求最小边长.
,求最小边长.