定义在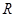 上的可导函数
上的可导函数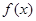 ,当
,当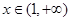 时,
时,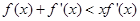 恒成立,
恒成立,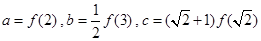 ,则
,则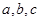 的大小关系为 ( )
的大小关系为 ( )
A. |
B.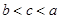 |
C.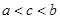 |
D.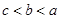 |
在△ 中,
中, 为△
为△ 的外心,则
的外心,则 等于
等于
A. |
B. |
C.12 | D.6 |
《莱因德纸草书》(Rh1nd Papyrus)是世界上最古老的数学著作之一,书中有这样的一道题目:把 个面包分给
个面包分给 个人,使每人所得成等差数列,且使较大的三份之和的
个人,使每人所得成等差数列,且使较大的三份之和的 是较小的两份之和,则最小
是较小的两份之和,则最小 份为
份为
A. |
B. |
C. |
D. |
把函数 的图象向左平移
的图象向左平移 个单位,所得图象的函数解析式是
个单位,所得图象的函数解析式是
A. |
B. |
C. |
D. |
若函数 的一个正数零点附近的函数值用二分法计算,其参考数据如下:
的一个正数零点附近的函数值用二分法计算,其参考数据如下:
| f(1) = -2 |
f(1.5) = 0.625 |
f(1.25) = -0.984 |
| f(1.375) = -0.260 |
f(1.4375) = 0.162 |
f(1.40625) = -0.054 |
那么方程 的一个近似根(精确到0.1)为
的一个近似根(精确到0.1)为
A.1.2 B.1.3 C.1.4 D.1.5
设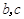 表示两条直线,
表示两条直线,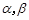 表示两个平面,则下列结论正确的是
表示两个平面,则下列结论正确的是
A.若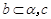 ∥ ∥ 则 则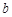 ∥ ∥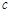 |
B.若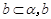 ∥ ∥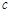 则 则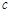 ∥ ∥ |
C.若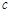 ∥ ∥ , , 则 则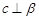 |
D.若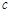 ∥ ∥ , ,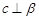 则 则 |