一辆汽车以10m/s的速率通过一座拱桥的桥顶,汽车对桥面的压力等于车重的一半,这座拱桥的半径是多少?若要使汽车过桥顶时对桥面无压力,则汽车过桥顶时的速度大小至少是多少?(取g ="10" m/s2)
如图所示的装置叫做阿特伍德机,是阿特伍德创制的一种著名力学实验装置,用来研究匀变速直线运动的规律。绳子两端的物体下落(上升)的加速度总是小于自由落体的加速度g,同自由落体相比,下落相同的高度,所花费的时间要长,这使得实验者有足够的时间从容的观测、研究。已知物体A、B的质量相等均为M,物体C的质量为m,轻绳与轻滑轮间的摩擦不计,轻绳不可伸长且足够长,如果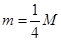 ,求:
,求: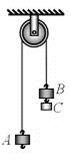
(1)物体B从静止开始下落一段距离的时间与其自由落体下落同样的距离所用时间的比值。
(2)系统在由静止释放后的运动过程中,物体C对B的拉力。
如图所示,一个质量为M=50kg的运动员和质量为m=10kg的木箱静止在光滑水平面上,从某时刻开始,运动员以vo=3m/s的速度向墙方向推出箱子,箱子与右侧墙壁发生完全弹性碰撞后返回,当运动员接刭箱子后,再次重复上述过程,每次运动员均以vo=3m/s的速度向墙方向推出箱子.求: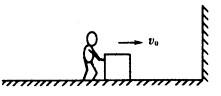
①运动员第一次接到木箱后的速度大小;
②运动员最多能够推出木箱几次?
一列简谐横波沿x轴传播,P为x=1m处的质点,振动传到P点开始计时,P点的振动图象如图甲所示.图乙为t=0.6s时的波动图象,求:
①该简谐横波的传播方向及波源的初始振动方向;
②波的传播速度.
如图所示,横截面积S=10cm2的活塞,将一定质量的理想气体封闭在竖直放置的圆柱形导热气缸内,开始活塞与气缸底都距离H=30cm.在活塞上放一重物,待整个系统稳定后.测得活塞与气缸底部距离变为h=25cm.已知外界大气压强始终为P0=1×105Pa,不计活塞质量及其与气缸之间的摩擦,取g=10rn/s2.求: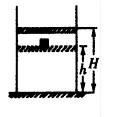
①所放重物的质量;
②在此过程中被封闭气体与外界交换的热量.
(12分)如图所示。在xOy平面直角坐标系内,y轴右侧有垂直纸面向里的匀强磁场,磁感应强度大小B=0.05T,虚线AC平行y轴,与y相距d=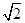 m,在x轴下方虚线与y轴所夹的区域存在如图所示的有界匀强电场,场强大小E=1V/m,方向与y轴成45o角,比荷
m,在x轴下方虚线与y轴所夹的区域存在如图所示的有界匀强电场,场强大小E=1V/m,方向与y轴成45o角,比荷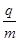 =102C/kg的带正电的粒子,从A(
=102C/kg的带正电的粒子,从A(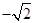 m,0)点静止释放.粒子所受重力不计.求:
m,0)点静止释放.粒子所受重力不计.求: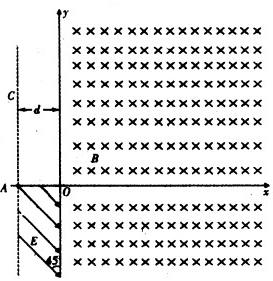
(1)粒子从释放到离开磁场所用时间.
(2)粒子再次到达虚线AC时的纵坐标.