水平地面上有一个半径为R的圆形跑道，高为h的平台边缘上P点在地面上P′点的正上方，P′与跑道圆心O的距离为L（L>R），P′AOC各点均在同一水平直线上，如图所示．一辆小车以速率v在跑道上顺时针运动，已知重力加速度为g，空气阻力不计，小沙袋、小车均可视为质点．则
（1）若从P点水平抛出小沙袋，使其落入小车中，小沙袋被抛出时的初速度v０应满足什么条件？
（2）若小车经过跑道上A点时（∠AOB＝90°），现从P点瞄准B点以某一水平初速度v1抛出小沙袋，使其落入小车中，则小沙袋被抛出时的初速度应满足什么条件？小车的速率 v应满足什么条件？
如图所示，质量相等的小球A、B分别固定在轻杆的中点及端点，当杆在光滑的水平面上绕O点匀速转动时，求杆的OA段及AB段对球的拉力大小之比．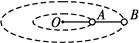
宇航员在地球表面以一定初速度竖直上抛一小球，经过时间t小球落回原处；若他在某星球表面以相同的初速度竖直上抛同一小球，需经过时间5t小球落回原处．(取地球表面重力加速度g＝10 m/s2，空气阻力不计)
(1)求该星球表面附近的重力加速度g′；
(2)已知该星球的半径与地球半径之比为R星∶R地＝1∶4，求该星球的质量与地球质量之比M星∶M地．
已知月球质量是地球质量的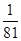
，月球半径是地球半径的
.求：
(1)在月球和地球表面附近，以同样的初速度分别竖直上抛一个物体时，上升的最大高度之比是多少？
(2)在距月球和地球表面相同高度处(此高度较小)，以同样的初速度分别水平抛出一个物体时，物体的水平射程之比为多少？
已知太阳的质量为M，地球的质量为m1，月球的质量为m2，设月亮到太阳的距离为a，地球到月亮的距离为b，则当发生日全食时，太阳对地球的引力F1和对月亮的吸引力F2的大小之比为多少？
月球环绕地球运动的轨道半径约为地球半径的60倍，其运行周期约为27天．现应用开普勒定律计算：在赤道平面内离地面多高时，人造地球卫星可随地球一起转动，就像其停留在天空中不动一样．若两颗人造卫星绕地球做圆周运动，周期之比为1∶8，则它们轨道半径之比是多少？(已知R地＝6.4×103 km)