已知等差数列 的前
的前 项和为
项和为 ,公差
,公差 ,且
,且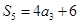 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设数列 是首项为1,公比为
是首项为1,公比为 的等比数列,求数列
的等比数列,求数列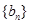 的前n项和
的前n项和 .
.
已知正四棱柱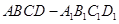 中,
中, 是
是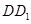 的中点.
的中点.
(1)求证: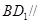 平面
平面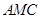 ;
;
(2)求证: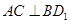 ;
;
(3)在线段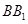 上是否存在点
上是否存在点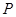 ,当
,当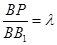 时,平面
时,平面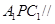 平面
平面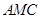 ?若存在,求出
?若存在,求出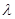 的值并证明;若不存在,请说明理由.
的值并证明;若不存在,请说明理由.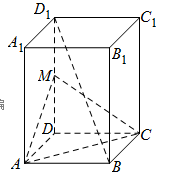
某学校为调查高一新生上学路程所需要的时间(单位:分钟),从高一年级新生中随机抽取100名新生按上学所需时间分组:第1组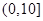 ,第2组
,第2组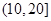 ,第3组
,第3组 ,第4组
,第4组 ,第5组
,第5组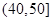 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示. 
(1)根据图中数据求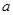 的值
的值
(2)若从第3,4,5组中用分层抽样的方法抽取6名新生参与交通安全问卷调查,应从第3,4,5组
各抽取多少名新生?
(3)在(2)的条件下,该校决定从这6名新生中随机抽取2名新生参加交通安全宣传活动,求第4组至少有一名志愿者被抽中的概率.
已知函数
 ,
, .
.
(1)求 的最小正周期及值域;
的最小正周期及值域;
(2)求 单调递增区间.
单调递增区间.
如图,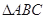 是边长为1的正三角形,
是边长为1的正三角形,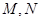 分别是边
分别是边 上的点,
上的点,
段 过
过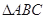 的重心
的重心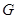 ,设
,设 .
.
(1)当 时,求
时,求 的长;
的长;
(2)分别记 的面积为
的面积为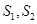 ,试将
,试将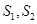 表示为
表示为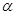 的函数;
的函数;
(3)求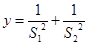 的最大值和最小值。
的最大值和最小值。