有一段“三段论”推理是这样的:对于可导函数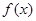 ,如果
,如果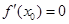 ,那么
,那么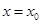 是函数
是函数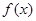 的极值点,因为函数
的极值点,因为函数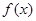 =
=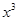 在x=0处的导数值
在x=0处的导数值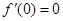 ,所以x=0是函数
,所以x=0是函数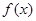 =
=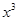 的极值点。以上推理中( )
的极值点。以上推理中( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |
直线 与
与 互相垂直,则
互相垂直,则 为
为
A. |
B.1 | C.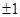 |
D. |
设有一个正方形网格,每个小正方形的边长为4,用直径等于1的硬币投掷到此网格上,硬币下落后与网格线没有公共点的概率为()
A. |
B. |
C. |
D. |
学校小卖部为了研究气温对饮料销售的影响,经过统计,得到一个卖出饮料数与当天气温的对比表:
| 摄氏温度 |
§-1 |
3 |
8 |
12 |
17 |
| 饮料瓶数 |
3 |
40 |
52 |
72 |
122 |
根据上表可得回归方程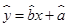 中的
中的 为6,据此模型预测气温为30℃时销售饮料瓶数为()
为6,据此模型预测气温为30℃时销售饮料瓶数为()
A.141B.191 C.211 D.241
圆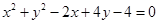 与直线
与直线
 的位置关系为()
的位置关系为()
| A.相离 | B.相切 | C.相交 | D.以上都有可能 |
某校现有高一学生210人,高二学生270人,高三学生300人,用分层抽样的方法从这三个年级的学生中随机抽取n名学生进行问卷调查,如果已知从高一学生中抽取的人数为7,那么从高三学生中抽取的人数应为()
| A.10 | B.9 | C.8 | D.7 |