如图甲所示,不计电阻的平行金属导轨竖直放置,导轨间距为L=1 m,上端接有电阻R=3 Ω,虚线OO′下方是垂直于导轨平面的匀强磁场,现将质量m=0.1 kg、电阻r=1 Ω的金属杆ab,从OO′上方某处垂直导轨由静止释放,杆下落过程中始终与导轨保持良好接触,杆下落过程中的v-t图象如图乙所示(取g=10 m/s2).求:
(1)磁感应强度B的大小.
(2)杆在磁场中下落0.1 s的过程中电阻R产生的热量.
(8 分).已知地球同步卫星离地面的高度约为地球半径的6倍。若某行星的平均密度为地球平均密度的一半,它的同步卫星距其表面的高度是其半径的2.5倍,求:该行星的自转周期。
如图所示,A是一个质量为1×10-3kg表面绝缘的薄板,薄板静止在光滑的水平面上,在薄板左端放置一质量为1×10-3kg带电量为q=1×10-5C的绝缘物块,在薄板上方有一水平电场,可以通过开关控制其有、无及方向.先产生一个方向水平向右,大小E1=3×102V/m的电场,薄板和物块开始运动,作用时间2s后,改变电场,电场大小变为E2=1×102V/m,方向向左,电场作用一段时间后,关闭电场,薄板正好到达目的地,物块刚好到达薄板的最右端,且薄板和物块的速度恰好为零. 已知薄板与物块间的动摩擦因数µ=0.1,(薄板不带电,物块体积大小不计,g取10m/s2)求: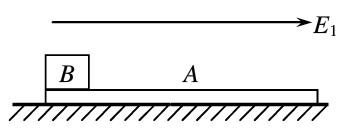
(1)在电场E1作用下物块和薄板的加速度各为多大;
(2)电场E2作用的时间;(3)薄板的长度和薄板移动的距离.
如图所示,真空中水平放置的两个相同极板Y和Y'长为L,相距d,足够大的竖直屏与两板右侧相距b.在两板间加上可调偏转电压U,一束质量为m、带电量为+q的粒子(不计重力)从两板左侧中点A以初速度v0沿水平方向射入电场且能穿出. 
(1)证明粒子飞出电场后的速度方向的反向延长线交于两板间的中心O点;
(2)求两板间所加偏转电压U的范围;
(3)求粒子可能到达屏上区域的长度.
如图甲所示,电荷量为q=1×10-4C的带正电的小物块置于绝缘水平面上,所在空间存在方向沿水平向右的电场,电场强度E的大小与时间的关系如图乙所示,物块运动速度与时间t的关系如图丙所示,取重力加速度g=10m/s2。求
(1)前2秒内物体加速度的大小;
(2)前4秒内物体的位移 ;
(3)前4秒内电场力做的功。
如图所示,R为电阻箱,V为理想电压表.当电阻箱读数为R1=2 Ω时,电压表读数为U1=4 V;当电阻箱读数为R2=5 Ω时,电压表读数为U2=5 V.求:
(1)电源的电动势E和内阻r;
(2)当电阻箱R读数为多少时,电源的输出功率最大?最大值Pm为多少?