小明在玩一副三角板时发现：含45°角的直角三角板的斜边可与含30°角的直角三角板的较长直角边完全重合（如图①）．即△C´DA´的顶点A´、C´分别与△BAC的顶点A、C重合．现在，他让△C´DA´固定不动，将△BAC通过变换使斜边BC经过△C´DA´的直角顶点D．
（1）如图②，将△BAC绕点C按顺时针方向旋转角度α（0°＜α＜180°），使BC边经过点D，则α＝ °．
（2）如图③，将△BAC绕点A按逆时针方向旋转，使BC边经过点D．试说明：BC∥A´C´．
（3）如图④，若AB＝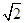
，将将△BAC沿射线A´C´方向平移m个单位长度，使BC边经过点D，求m的值．
如图，抛物线经过A（4，0）、B（1，0）、C（0，-2）三点．
（1）求出抛物线的解析式；
（2）在直线AC上方的抛物线上有一动点D，当△ACD的面积最大时，求出点D的坐标；
（3）P是抛物线上一动点，过P作PM⊥x轴，垂足为M，是否存在P点，使得以A，P，M为顶点的三角形与△OAC相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．
如图，在矩形ABCD的对角线AC上有一动点O，以OA为半径作⊙O交AD、AC于点E、F，连结CE．
（1）若CE恰为⊙O的切线，求证：∠ACB=∠DCE；
（2）在（1）的条件下，若AB=
，BC=2，求⊙O的半径．
如图，已知AB是⊙O的直径，直线CD与⊙O相切于点C，AC平分∠DAB．
（1）求证：AD⊥DC；
（2）若AD=2，AC=
，求AB的长．
已知矩形ABCD的一条边AD=8，将矩形ABCD折叠，使得顶点B落在CD边上的P点处．如图，已知折痕与边BC交于O，连结AP、OP、OA．
（1）求证：△OCP∽△PDA；
（2）若△OCP与△PDA的面积比为1：4，求边AB的长；
如图，在△ABC中，AD是角平分钱，点E在AC上，且∠EAD=∠ADE．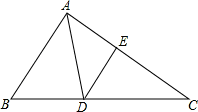
（1）求证：△DCE∽△BCA；
（2）若AB=3，AC=4．求DE的长．