如图所示,斜面上有A、B、C、D四个点,AB=BC=CD,从A点以初动能Ek0水平抛出一个小球,它落在斜面上的B点,速度方向与斜面之间的夹角为θ,若小球从A点以初动能2Ek0水平抛出,不计空气阻力,则下列判断正确的是( )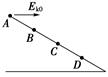
| A.小球将落在C点 |
| B.小球将落在C下方 |
| C.小球落在斜面的速度方向与斜面的夹角大于θ |
| D.小球落在斜面的速度方向与斜面的夹角等于θ |
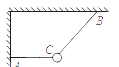
.如图所示的装置,用两根细绳拉住一个小球,两细绳间的夹角为θ,细绳AC呈水平状态.现将整个装置在纸面内顺时针缓慢转动,共转过90°.在转动的过程中,CA绳中的拉力F1和CB绳中的拉力F2的大小发生变化,即
| A.F1先变小后变大 | B.F1先变大后变小 |
| C.F2逐渐减小 | D.F2最后减小到零 |
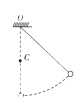
细绳的一端固定于O点,另一端系一小球,在O点的正下方钉一个钉子C,如图所示。小球从一定高度摆下,不考虑细绳的质量和形变,细绳与钉子相碰前后下述说法中正确的是
| A.将钉子向下移动绳子容易断 |
| B.小球的向心加速度不变 |
| C.绳子的拉力变大 |
| D.小球的线速度增大 |
一重球从高h处下落,如图所示,到A点时接触弹簧,压缩弹簧至最低点位置B。那么重球从A至B的运动过程中
A、速度一直减小
B、速度先增加后减小
C、在B处加速度可能为零
D、加速度方向先竖直向下再竖直向上
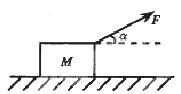
如图所示,放在水平地面上质量为M的小木块,木块与地面之间的动摩擦因数为μ,当地的重力加速度为g。在大小为F、方向与水平方向成α角的拉力作用下能够沿着地面做匀加速直线运动,则木块的加速度大小为
| A.F/M |
| B.Fcosα/M |
| C.(Fcosα-μMg)/M |
| D.(Fcosα+μFsinα-μMg)/M |
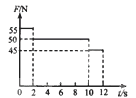
将重为50N的物体放在某直升电梯的地板上。该电梯在经过某一楼层地面前后运动过程中,物体受到电梯地板的支持力随时间变化的图象如图所示。由此可以判断
| A.t=1s时刻电梯的加速度方向竖直向下 |
| B.t=6s时刻电梯的加速度为零[ |
| C.t=8s时刻电梯处于失重状态 |
| D.t=11s时刻电梯的加速度方向竖直向上 |