某学校为调查高二年级学生的身高情况,按随机抽样的方法抽取200名学生,得到男生身高情况的频率分布直方图(图(1))和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在170~175cm的男生人数有48人.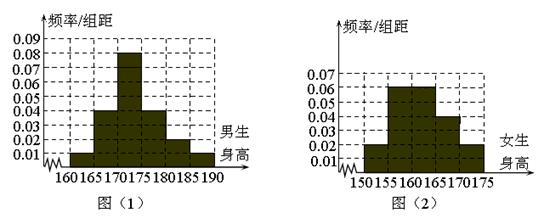 (Ⅰ)在抽取的学生中,身高不超过165cm的男、女生各有多少人?并估计男生的平均身高。
(Ⅰ)在抽取的学生中,身高不超过165cm的男、女生各有多少人?并估计男生的平均身高。
(Ⅱ)在上述200名学生中,从身高在170~175cm之间的学生按男、女性别分层抽样的方法,抽出7人,从这7人中选派4人当旗手,求4人中至少有一名女生的概率.
某校为了探索一种新的教学模式,进行了一项课题实验,甲班为实验班,乙班为对比班,甲乙两班的人数均为50人,一年后对两班进行测试,测试成绩的分组区间为[80,90)、[90,100)、[100,110)、[110,120)、[120,130),由此得到两个班测试成绩的频率分布直方图: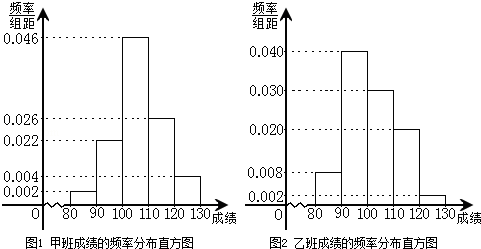
(Ⅰ)完成下面2×2列联表,你能有97.5%的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由;
| 成绩小于100分 |
成绩不小于100分 |
合计 |
|
| 甲班 |
a= _________ |
b= _________ |
50 |
| 乙班 |
c=24 |
d=26 |
50 |
| 合计 |
e= _________ |
f= _________ |
100 |
附:K2= ,其中n=a+b+c+d
,其中n=a+b+c+d
| P(K2≥k0) |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k0 |
2.072 |
2.706 |
3.841 |
5.204 |
6.635 |
7.879 |
10.828 |
设函数f(x)=ax3+bx2+c,其中a+b=0,a,b,c均为常数,曲线y=f(x)在(1,f(1))处的切线方程为x+y﹣1=0.
(Ⅰ)求a,b,c的值;
(Ⅱ)求函数f(x)的单调区间.
某公司近年来科研费用支出x万元与公司所获得利润y万元之间有如下的统计数据:
| x |
2 |
3 |
4 |
5 |
| Y |
18 |
27 |
32 |
35 |
(Ⅰ)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程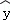 =
= x+
x+ ;
;
(Ⅱ)试根据(2)求出的线性回归方程,预测该公司科研费用支出为10万元时公司所获得的利润.
参考公式:若变量x和y用最小二乘法求出y关于x的线性回归方程为: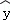 =
= x+
x+ ,其中:
,其中: =
=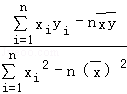 ,
, =
= ﹣
﹣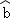
 ,参考数值:2×18+3×27+4×32+5×35=420.
,参考数值:2×18+3×27+4×32+5×35=420.
(Ⅰ)求证: +
+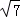 <2
<2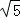
(Ⅱ)已知a>0,b>0且a+b>2,求证: ,
,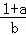 中至少有一个小于2.
中至少有一个小于2.
已知复数z=1﹣i(i是虚数单位)
(Ⅰ)计算z2;
(Ⅱ)若z2+a ,求实数a,b的值.
,求实数a,b的值.