在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
①△DFE是等腰直角三角形;
②四边形CEDF不可能为正方形;
③四边形CEDF的面积随点E位置的改变而发生变化;
④点C到线段EF的最大距离为 .
.
其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
下列“QQ表情”中,属于轴对称图形的是()
如图是一个简单的数值运算程序,当输入的 的值为-1时,则输出的值为()
的值为-1时,则输出的值为()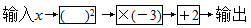
| A.1 | B.-5 | C.-1 | D.5 |
在△ABC中,∠C为锐角,分别以AB,AC为直径作半圆,过点B,A,C作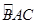 ,如图所示.若AB=4,AC=2,S1﹣S2=
,如图所示.若AB=4,AC=2,S1﹣S2=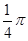 ,则S3﹣S4的值是()
,则S3﹣S4的值是()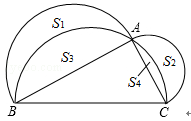
A.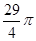 |
B.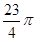 |
C.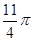 |
D.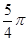 |
向东行驶3km,记作+3km,向西行驶2km记作()
| A.+2km | B.﹣2km | C.+3km | D.﹣3km |
近年来,随着交通网络的不断完善,我市近郊游持续升温。 据统计,在今年“五一”期间,某风景区接待游览的人数约为20.3万人,这一数据用科学记数法表示为()
A. 人 人 |
B. 人 人 |
C.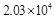 人 人 |
D.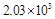 人 人 |