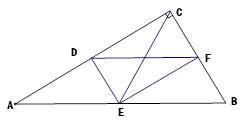
运用“同一图形的面积不同表示方式相同”可以证明一类含有线段的等式，这种解决问题的方法我们称之为面积法．
（1）如图，在等腰三角形ABC中，AB=AC，AC边上的高为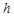
，M是底边BC上的任意一点，点M到腰AB、AC的距离分别为
、
．连接AM,可得结论
+
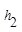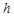=．当点M在BC延长线上时，
、
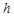、之间的等量关系式是 ．（直接写出结论不必证明）．
（2）应用：平面直角坐标系中有两条直线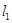
：
、
：
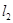，若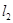上的一点M到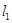的距离是1．请运用（1）的条件和结论求出点M的坐标．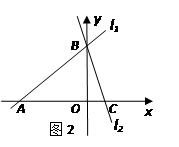
（1）计算：
；（2）求x的值：
.
已知：如图，在四边形ABCD中，∠ABC＝90°，CD⊥AD，AD2＋CD2＝2AB2．
（1）求证：AB＝BC；
（2）当BE⊥AD于E时，试证明：BE＝AE＋CD．
平行四边形两个顶点坐标分别为（-3，0），（1，0），第3个顶点在y轴上，且与x轴的距离为3个单位长度.求第4个顶点的坐标.
如图，AB两地相距50千米，甲于某日下午1时骑自行车从A地出发驶往B地，乙也于同日下午骑摩托车从A地出发驶往B地，图中PQR和线段MN，分别表示甲和乙所行驶的路程S与该日下午时间t之间的关系，试根据图形回答：
（1）甲出发几小时，乙才开始出发？
（2）乙行驶多少分钟赶上甲，这时两人离B地还有多少千米？
（3）甲从下午2时到5时的速度是多少？
（4）乙行驶的速度是多少？
如图，已知在△ABC中，∠ACB=90°，点D、E、F分别是AC、AB、BC的中点，
试说明：CE=DF.