在xoy平面内，直线OP与y轴的夹角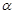
=45o。第一、第二象限内存在大小相等，方向分别为竖直向下和水平向右的匀强电场,电场强度E=1.0×105N/C ；在x轴下方有垂直于纸面向外的匀强磁场，磁感应强度B=0.1T，如图所示。现有一带正电的粒子从直线OP上某点A（-L, L）处静止释放。设粒子的比荷
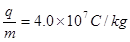，粒子重力不计。求：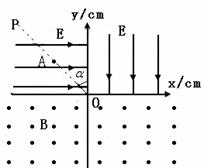
（1）当L=2cm时，粒子进入磁场时与x轴交点的横坐标
（2）当L=2cm时，粒子进入磁场时速度的大小和方向
（3）如果在直线OP上各点释放许多个上述带电粒子（粒子间的相互作用力不计），试证明各带电粒子进入磁场后做圆周运动的圆心点的集合为一抛物线（提示：写出圆心点坐标x、y的函数关系）
质量为m=1kg的小物块轻轻放在水平匀速运动的传送带上的P点，随传送带运动到A点后水平抛出，小物块恰好无碰撞的沿圆弧切线从B点进入竖直光滑圆孤轨道下滑。B、C为圆弧的两端点，其连线水平，斜面与圆弧轨道在C点相切连接（小物块经过C点时机械能损失不计）。已知圆弧半径R=1．0 m，圆弧对应圆心角
，轨道最低点为O，A点距水平面的高度h=0．8m。设小物块首次经过C点时为零时刻，在t=0．8s时刻小物块经过D点，小物块与斜面间的滑动摩擦因数为
=
。（g=10m/s2，sin37°=0．6，cos37°=
0．8）试求：
（1）小物块离开A点的水平初速度v1大小；
（2）小物块经过O点时对轨道的压力；
（3）斜面上CD间的距离。
在光滑的地面上，小球A以速率v0向右运动时跟静止的小球B发生碰撞，碰后A球以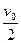
的速率弹回，而B球以
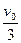的速率向右运动，求
（1）A、B两球的质量之比；
（2）请你判断该碰撞是否为弹性碰撞。
为了安全，在公路上行驶的汽车之间应保持必要的距离，已知某高速公路的最高限速为108 km/h假设前方车辆突然停止，后车司机从发现这一情况经操纵刹车，到汽车开始减速所经历的时间(即反应时间)t＝0.50s，刹车时汽车加速度的大小为5m/s2，该高速公路上汽车间的距离至少应为多少？
水滴自屋檐由静止落下，经过高为1.8米的窗口历时0.2秒，若空气阻力不计，屋檐离窗顶多高？（g=10m/s2）
一质点做匀加速直线运动，经4 s通过的位移是24 m，速度达到11 m/s，，求质点运动的初速度和加速度。