若(a+1)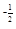 <(3-2a)
<(3-2a)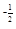 ,则a的取值范围是__________.
,则a的取值范围是__________.
已知集合A={(x,y)|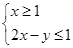 },集合B={(x,y)|3x+2y-m=0},若A∩B
},集合B={(x,y)|3x+2y-m=0},若A∩B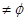 ,则实数m 的最小值等于__________.
,则实数m 的最小值等于__________.
对于数列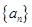
 ,若
,若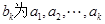 中最大值
中最大值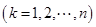 ,则称数列
,则称数列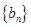 为数列
为数列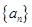 的“凸值数列”.如数列2,1,3,7,5的“凸值数列”为2,2,3,7,7;由此定义,下列说法正确的有___________________.
的“凸值数列”.如数列2,1,3,7,5的“凸值数列”为2,2,3,7,7;由此定义,下列说法正确的有___________________.
①递减数列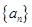 的“凸值数列”是常数列;②不存在数列
的“凸值数列”是常数列;②不存在数列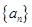 ,它的“凸值数列”还是
,它的“凸值数列”还是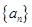 本身;③任意数列
本身;③任意数列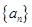 的“凸值数列”是递增数列;④“凸值数列”为1,3,3,9的所有数列
的“凸值数列”是递增数列;④“凸值数列”为1,3,3,9的所有数列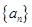 的个数为3.
的个数为3.
原命题:“设 ”以及它的逆命题,否命题,逆否命题中,真命题的个数是______________________.
”以及它的逆命题,否命题,逆否命题中,真命题的个数是______________________.
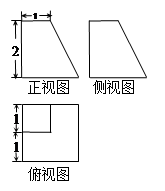
某四棱台的三视图如图所示,则该四棱台的体积为__________.