作图题: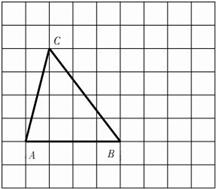
(1)在单位长度为1方格纸中,将△ABC向右平移3个单位得到△A1B1C1,画出△A1B1C1.
(2)求△A1B1C1的面积
计算:7.5+(-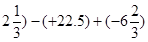
下表是某一周某种股票每天的收盘价(收盘价:股票每天交易结束时的价格)
| 时间 |
星期一 |
星期二 |
星期三 |
星期四 |
星期五 |
| 收盘价(元/股) |
13.4 |
13.4 |
|||
| 比前一天涨跌(元/股) |
/ |
-0.02 |
+0.06 |
-0.25 |
(1)填表,并回答哪天收盘价最高?哪天收盘价最低?
(2)最高价与最低价相差多少?
某校初二年级(1)班的学生的平均体重50㎏。
(1)下表给出了该班5名同学的体重情况(单位:㎏)试完成下表:
| 姓名 |
小张 |
小王 |
小李 |
小山 |
小毛 |
| 体重 |
55 |
45 |
|||
| 体重与平均体重差 |
+5 |
+2 |
+1 |
-3 |
(2)谁最重?谁最轻?
(3)最重与最轻相差多少?
(8分)水果市场某批发商经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)现要保证每天盈利6000元,同时又要让顾客尽可能多得到实惠,那么每千克应涨价多少元?
(2)若该批发商单纯从经济角度看,那么每千克应涨价多少元,能使商场获利最多?
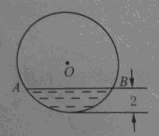
(8分)如图,水平放置的圆柱形排水管的截面为⊙O,有水部分弓形的高为2,弦AB=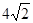
(1)求⊙O的半径;
(2)求截面中有水部分弓形的面积。(保留根号及π)