如图所示，装置BO′O可绕竖直轴O′O转动，可视为质点的小球A与两细线连接后分别系于B、C两点，装置静止时细线AB水平，细线AC与竖直方向的夹角θ=37º．已知小球的质量m=1kg，细线AC长l=1m， B点距C点的水平和竖直距离相等．（重力加速度g取10m/s2，
，
）（结果可以用根号表示）
（1）若装置匀速转动的角速度为ω1时，细线AB上的张力为零而细线AC与竖直方向夹角仍为37º，求角速度ω1的大小；
（2）若装置匀速转动的角速度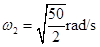
，求细线AC与竖直方向的夹角的余弦值；
（3）装置可以以不同的角速度匀速转动，试通过计算在坐标图中画出细线AC上张力T随角速度的平方ω2 变化的关系图象。
如图所示，在真空中有一与x轴平行的匀强电场，一电子由坐标原点O处以速度v0沿y轴正方向射入电场，在运动中该电子通过位于xoy平面内的A点，A点与原点O相距L，OA与x轴方向的夹角为θ，已知电子电量q=-1.6×10-19C，电子质量m=9×10-31kg，初速度v0=1×107m/s，O与A间距L=10cm、θ=30º。求匀强电场的场强大小和方向。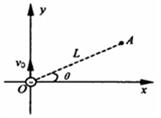
一个电子以与电场方向相同的初速度υ0，射入电场强度为E的匀强电场中，如图所示，已知电子电量e，电子质量m，试求：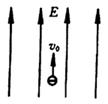
(1) 电子的入射点与速度为零之点间的电势差和这两点间的距离?
(2) 从电子的入射点到速度为零之点所需的时间?
如图所示的直角坐标系中，第Ⅰ、Ⅳ象限内存在着垂直纸面向里的匀强磁场，在x＝－2L与y轴之间第Ⅱ、III象限内存在大小相等，方向相反的匀强电场，场强方向如图所示。在A(－2L，L)到C(－2L,0)的连线上连续分布着电荷量为＋q、质量为m的粒子。从t＝0时刻起，这些带电粒子依次以相同的速度v0沿x轴正方向射出。从A点射出的粒子刚好沿如图所示的运动轨迹（轨迹与x轴的交点为OC的中点）从y轴上A′(0，－L)沿x轴正方向进入磁场。不计粒子的重力及它们间的相互作用，不考虑粒子间的碰撞。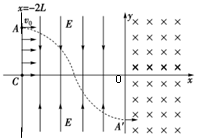 
(1)求电场强度E的大小；
(2)若匀强磁场的磁感应强度
,求从A′点进入磁场的粒子返回到直线x＝－2L时的位置坐标；
(3)在AC间还有哪些位置的粒子，经过电场后也能沿x轴正方向进入磁场。
我人民海军进行某次登陆演练，假设一艘战舰因吨位大，吃水太深，只能停锚在离海岸某处。登陆队员需要从较高的军舰甲板上，利用绳索下滑到登陆快艇上再行登陆接近目标，若绳索两端固定好后，与竖直方向的夹角θ=30°，队员甲先匀加速滑到某最大速度，再靠摩擦匀减速滑至快艇，速度刚好为零，在队员甲开始下滑时，队员乙在甲板上同时从同一地点开始向快艇以速度v0=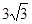
m／s平抛救生圈，第一个刚落到快艇上时，紧接着抛第二个，结果第二个救生圈刚好与甲队员同时抵达快艇上的同一位置，取g=10m／s2，不计空气阻力，求：
(1)军舰甲板到快艇的竖直高度H；
(2)队员甲在绳索上运动的时间t0及队员甲在下滑过程中的最大速度v1；
(3)若登陆快艇一开始停在离海岸S=1km处（如图），登陆快艇额定功率P=5kw，载人后连同装备总质量m=103kg，从静止开始以额定功率向登陆点加速靠近，到达岸边时刚好能达到最大速度v2=10m／s，求登陆艇运动的时间t'。
如图甲所示，一半径R＝1m、圆心角等于143°的竖直圆弧形光滑轨道，与斜面相切于B处，圆弧轨道的最高点为M，斜面倾角θ＝37°，t＝0时刻有一物块从斜面底端A处沿斜面上滑，其在斜面上运动的速度变化规律如图乙所示．若物块恰能到达M点，(取g＝10m/s2，sin37°＝0.6，cos37°＝0.8)，求：
(1)物块经过B点时的速度；
(2)物块与斜面间的动摩擦因数μ.