设A1,A2,A3,A4,A5是平面上给定的5个不同点,则使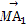 +
+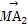 +
+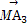 +
+ +
+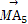 =0成立的点M的个数为( )
=0成立的点M的个数为( )
| A.0 | B.1 | C.5 | D.10 |
已知点P为△ABC所在平面上的一点,且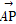 =
=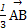 +t
+t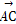 ,其中t为实数,若点P落在△ABC的内部,则t的取值范围是( )
,其中t为实数,若点P落在△ABC的内部,则t的取值范围是( )
A.0<t< |
B.0<t< |
C.0<t< |
D.0<t< |
如图,平面内有三个向量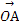 ,
,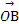 ,
, ,其中
,其中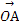 与
与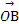 的夹角为120°,
的夹角为120°,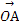 与
与 的夹角为30°,且|
的夹角为30°,且|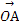 |=|
|=|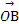 |=1,|
|=1,| |=2
|=2 ,若
,若 =λ
=λ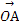 +μ
+μ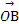 (λ,μ∈R),则λ+μ的值为( )
(λ,μ∈R),则λ+μ的值为( )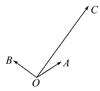
| A.4 | B.5 | C.6 | D.8 |
在△ABC中, =2
=2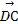 ,
,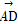 =m
=m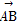 +n
+n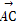 ,则
,则 的值为( )
的值为( )
| A.2 | B. |
C.3 | D. |
已知a,b是不共线的向量,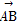 =λa+b,
=λa+b,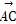 =a+μb(λ,μ∈R),那么A,B,C三点共线的充要条件是( )
=a+μb(λ,μ∈R),那么A,B,C三点共线的充要条件是( )
| A.λ+μ=2 | B.λ-μ=1 |
| C.λμ=-1 | D.λμ=1 |