如图,已知关于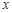 的一元二次函数
的一元二次函数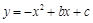 (
(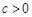 )的图象与
)的图象与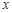 轴相交于
轴相交于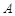 、
、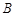 两点(点
两点(点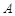 在点
在点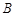 的左侧),与
的左侧),与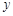 轴交于点
轴交于点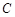 ,且
,且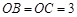 ,顶点为
,顶点为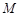 .
.
(1)求出一元二次函数的关系式;
(2)点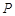 为线段
为线段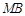 上的一个动点,过点
上的一个动点,过点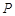 作
作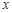 轴的垂线
轴的垂线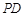 ,垂足为
,垂足为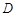 .若
.若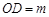 ,
,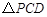 的面积为
的面积为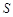 ,求
,求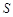 关于
关于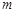 的函数关系式,并写出
的函数关系式,并写出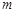 的取值范围;
的取值范围;
(3)在(2)的条件下,当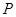 点坐标是 时,
点坐标是 时, 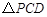 为直角三角形.
为直角三角形.
解下列方程
(1)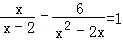
(2)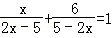 .
.
化简
(1)
(2) .
.
某校餐厅计划购买12张餐桌和一批餐椅,现从甲、乙两商场了解到:同一型号的餐桌报价每张均为200元,餐椅报价每把均为50元.甲商场称:每购买一张餐桌赠送一把餐椅;乙商场规定:所有餐桌椅均按报价的八五折销售.那么,什么情况下到甲商场购买更优惠?
已知:如图,把长方形纸片ABCD沿EF折叠后.点D与点B重合,点C落在点C′的位置上.若∠1=60°,AE=1.
(1)求∠2、∠3的度数;
(2)求长方形纸片ABCD的面积S.
为了了解中学生的体能情况,抽取了某中学八年级学生进行跳绳测试,将所得数据整理后,画出如图所示的频率分布直方图,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数为5。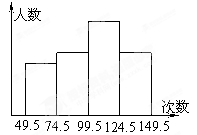
(1)第四小组的频率是__________;
(2)参加这次测试的学生是_________人;
(3)成绩落在哪组数据范围内的人数最多?是多少?
(4)求成绩在100次以上(包括100次)的学生占测试人数的百分率.