在 中,
中, ,
, ,将一块等腰直角三角板的直角顶点放在斜边
,将一块等腰直角三角板的直角顶点放在斜边 的中点
的中点 处,将三角板绕点
处,将三角板绕点 旋转,三角板的两直角边分别交射线
旋转,三角板的两直角边分别交射线 、
、 于
于 、
、 两点. 如图①、②、③是旋转三角板得到的图形中的三种情况,试探究:
两点. 如图①、②、③是旋转三角板得到的图形中的三种情况,试探究:
(1)三角板绕点 旋转,观察线段
旋转,观察线段 和
和 之间有什么数量关系?并结合图②加以证明;
之间有什么数量关系?并结合图②加以证明;
(2)三角板绕点 旋转,
旋转, 是否能成为等腰三角形?若能,写出所有
是否能成为等腰三角形?若能,写出所有 为等腰三角形时
为等腰三角形时 的长(直接写出答案即可);若不能,请说明理由;
的长(直接写出答案即可);若不能,请说明理由;
(3)如图 ,若将三角板的直角顶点放在斜边
,若将三角板的直角顶点放在斜边 上的
上的 处,且
处,且 ,和前面一样操作,试问线段
,和前面一样操作,试问线段 和
和 之间有什么数量关系?并结合图④证明你的结论.
之间有什么数量关系?并结合图④证明你的结论.
(12分)2007年我市某县筹备20周年县庆,园林部门决定利用现有的3490盆甲种花卉和295 0盆乙种花卉搭配
0盆乙种花卉搭配 两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个
两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个 种造型需甲种花卉80盆,乙种花卉40盆,搭配一个
种造型需甲种花卉80盆,乙种花卉40盆,搭配一个 种造型需甲种花卉50盆,乙种花卉90盆.
种造型需甲种花卉50盆,乙种花卉90盆.
(1)某校九年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来.
(2)若搭配一个 种造型的成本是800元,搭配一个
种造型的成本是800元,搭配一个 种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?
种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?
. (10分)今年春季,我国云南、贵州等西南地区遇到多少不遇旱灾,“一方有难,八方支援”,为及时灌溉农田,丰收农机公司决定支援上坪村甲、乙、丙三种不同功率柴油发电机共10台(每种至少一台)及配套相同型号抽水机4台、3台、2台,每台抽水机每小时可抽水灌溉农田1亩.现要求所有柴油发电机及配套抽水机同时工作一小时,灌溉农田32亩.
(10分)今年春季,我国云南、贵州等西南地区遇到多少不遇旱灾,“一方有难,八方支援”,为及时灌溉农田,丰收农机公司决定支援上坪村甲、乙、丙三种不同功率柴油发电机共10台(每种至少一台)及配套相同型号抽水机4台、3台、2台,每台抽水机每小时可抽水灌溉农田1亩.现要求所有柴油发电机及配套抽水机同时工作一小时,灌溉农田32亩.
(1)设甲种柴油发电机数量为x台,乙种柴油发电机数量为y台.
①用含x、y的式子表示丙种柴油发电机的数量;
②求出y与x的关系式;
(2)已知甲、乙、丙柴油发电机每台每小时费用分别为130元、120元、100元,应如何安排三种柴油发电机的数量,既能按要求抽水灌溉,同时柴油发电机总费用W最少?
(10分)某学校组织八年级学生参加社会实践活动,若单独租用35座客车若干辆,则刚好坐满;若单独租用55座客车,则可以少租一辆,且余45个空座位.
(1)求该校八年级学生参加社会实践活动的人数;
(2)已知35座客车的租金为每辆320元,55座客车的租金为每辆400元.根据租车资金不超过1500元的预算,学校决定同时租用这两种客车共4辆(可以坐不满).请你计算本次社会实践活动所需车辆的租金.
(8分)已知不等式:⑴1-x<0;⑵ <1;⑶ 2x+3>1;⑷ 0.2x-3<-2.你喜欢其中哪两个不等式,请把它们选出来组成一个不等式组,求出它的解集,并在数轴上把解集表示出来
<1;⑶ 2x+3>1;⑷ 0.2x-3<-2.你喜欢其中哪两个不等式,请把它们选出来组成一个不等式组,求出它的解集,并在数轴上把解集表示出来
(8分)解不等式组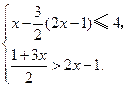 把解集表示在数轴上,并求出不等式组的整数解.
把解集表示在数轴上,并求出不等式组的整数解.