阅读下面材料:
根据两角和与差的正弦公式,有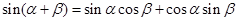 ①
①
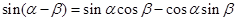 ②
②
由①+②得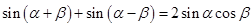 ③
③
令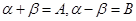 有
有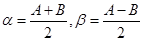
代入③得 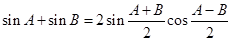 .
.
(Ⅰ)类比上述推理方法,根据两角和与差的余弦公式,证明:
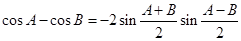 ;
;
(Ⅱ)若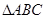 的三个内角
的三个内角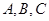 满足
满足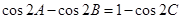 ,试判断
,试判断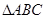 的形状.(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
的形状.(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
(满分12分)已知函数 的单调递减区间是(1,2),且满足
的单调递减区间是(1,2),且满足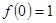 。
。
(1)求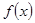 的解析式;
的解析式;
(2)对任意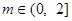 ,关于
,关于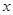 的不等式
的不等式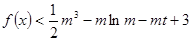 在
在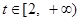 上有解,求实数
上有解,求实数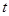 的取值范围。
的取值范围。
(满分12分)已知圆O: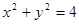 ,点P在直线
,点P在直线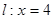 上的动点。
上的动点。
(1)若从P到圆O的切线长为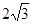 ,求P点的坐标以及两条切线所夹劣弧长;
,求P点的坐标以及两条切线所夹劣弧长;
(2)若点A(-2,0),B(2,0),直线PA,PB与圆O的另一个交点分别为M,N,求证:直线MN经过定点(1,0)。
(满分12分)定义在R上的奇函数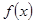 有最小正周期4,且
有最小正周期4,且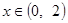 时,
时,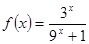 。
。
(1)求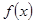 在
在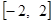 上的解析式;
上的解析式;
(2)判断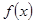 在(0,2)上的单调性,并给予证明;
在(0,2)上的单调性,并给予证明;
(3)当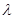 为何值时,关于方程
为何值时,关于方程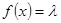 在
在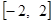 上有实数解?
上有实数解?
(满分12分) 是等差数列
是等差数列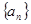 的前
的前 项和,
项和, ,
, 。
。
(1)求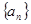 的通项公式;
的通项公式;
(2)设 (
(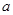 是实常数,且
是实常数,且 ),求
),求 的前
的前 项和
项和 。
。
(满分12分)设命题P:关于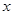 的不等式:
的不等式: 的解集是R,命题Q:函数
的解集是R,命题Q:函数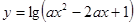 的定义域为R,若P或Q为真,P且Q为假,求
的定义域为R,若P或Q为真,P且Q为假,求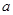 的取值范围。
的取值范围。