为了美观，在加工太阳镜时将下半部分轮廓制作成抛物线的形状（如图所示）．对应的两条抛物线关于y轴对称，AE∥x轴，AB＝4cm，最低点C在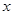
轴上，高CH＝1cm，BD＝2cm．则右轮廓线DFE所在抛物线的函数解析式为（ ）
A． |
B． |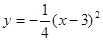
C． |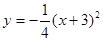
D． |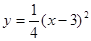
若△ABC∽△A′B′C′，相似比为1︰2，则△ABC与△A′B′C′的面积的比为( )
| A．1︰2 | B．2︰1 |
| C．1︰4 | D．4︰1 |
如图，D，E分别是△ABC的边AB，AC上的点，∠B＝∠1，AE＝EC＝4，BC＝10，AB＝12，则△ADE和△ACB的周长之比为( )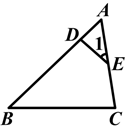
| A．1︰2 | B．1︰3 |
| C．1︰4 | D．1︰5 |
在Rt△ABC和Rt△A′B′C′中，∠C＝∠C′＝90°，若添加一个条件，使得Rt△ABC∽Rt△A′B′C′，则下列条件中不符合要求的是（ ）
| A．∠A＝∠A′ | B．∠B＝∠B′ |
C． |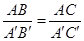
D． |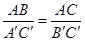
如图，已知∠1＝∠2，那么添加下列一个条件后，仍无法判定△ABC∽△ADE的是（ ）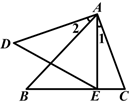
A． |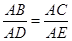
B．∠C＝∠AED |
| C．∠B＝∠D | D． |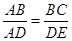
在△ABC与△A′B′C′中，AB︰AC＝A′B′︰A′C′，∠B＝∠B′，则这两个三角形（ ）
| A．相似，但不全等 | B．全等或相似 |
| C．不相似 | D．无法判定是否相似 |