某实验小组利用如下图所示的实验装置来探究当合外力一定时,物体运动的加速度与其质量之间的关系。
(1)实验前用刻度尺测出两个光电门中心之间的距离s,并测得遮光条的宽度d。该实验小组在做实验时,将滑块从图所示位置由静止释放,由数字计时器可以读出遮光条通过光电门1的时间Δt1,遮光条通过光电门2的时间Δt2,则滑块经过光电门1时的瞬时速度的表达式v1= ,滑块经过光电门2时的瞬时速度的表达式v2= ,则滑块的加速度的表达式a= 。(以上表达式均用直接测量的物理量的字母表示)。
(2)在本次实验中,实验小组通过改变滑块质量做了6组实验,得到如下表所示的实验数据。
| 实验次数 |
1 |
2 |
3 |
4 |
5 |
6 |
| 质量m(g) |
250 |
300 |
350 |
400 |
500 |
800 |
| 加速度a( m/s2 ) |
2.02 |
1.65 |
1.43 |
1.25 |
1.00 |
0.63 |
通过计算分析上表数据后,得出的结论是在合外力不变的情况下,物体运动的加速度跟物体的质量成反比,如果想通过图象法进一步确认自己的结论,须建立 (填a—m或a— )坐标系,根据实验数据描点作图,如果图线是一条 ,就可确认上述结论。
)坐标系,根据实验数据描点作图,如果图线是一条 ,就可确认上述结论。
伽利略为了研究自由落体的规律,将落体实验转化为著名的“斜面实验”,从而创造了一种科学研究的方法.利用斜面实验主要是考虑到()
| A.实验时便于测量小球运动的速度 |
| B.实验时便于测量小球运动的时间 |
| C.实验时便于测量小球运动的路程 |
| D.斜面实验可以通过观察与计算直接得到落体的运动规律 |
在研究匀变速直线运动的实验中,算出小车经过各计数点瞬时速度如下
| 计数点序号 |
1 |
2 |
3 |
4 |
5 |
6 |
| 计数点对应的时刻(s) |
0.10 |
0.20 |
0.30 |
0.40 |
0.50 |
0.60 |
| 通过计数点的速度(cm/s) |
44.0 |
62.0 |
81.0 |
100.0 |
110.0 |
168.0 |
为了计算加速度,合理的方法是()
A.根据任意两计数点的速度用公式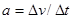 算出加速度
算出加速度
B.根据实验数据画出v-t图,量出其倾角,由公式a = tan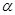 求出加速度
求出加速度
C.根据实验数据画出v-t图,由图线上相距较远的两点所对应的速度、时间,用公式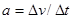 算出加速度
算出加速度
D.依次算出通过连续两计数点间的加速度,算出平均值作为小车的加速度
如图所示,物体自O点由静止开始做匀加速直线运动,A、B、C、D为其运动轨迹上的四点,测得AB="2" m,BC="3" m.且物体通过AB、BC、CD所用的时间相等,则下列说法正确的是( )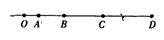
A. 可以求出物体加速度的大小
B. 可以求得CD=4m
C. 可以求得OA之间的距离为1.125 m
D. 可以求得OB之间的距离为12.5 m
如图所示,选沿斜面向上为正方向,小球以v0=20m/s、加速度为a=-5m/s2,从A点沿光滑斜面一直做匀变速直线运动,斜面长L=40m.求小球经过斜面中点C需要的时间( )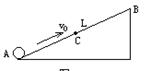
| A.2s | B.6.828s | C.2.586s | D.1.172s |
火车在平直轨道上做匀变速直线运动,经过时间t,它的速度由 变为
变为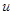 ,经过的位移为x,下列说法正确的是( )
,经过的位移为x,下列说法正确的是( )
| A.这段时间内的平均速度等于x/t | B.这段时间内的平均速度等于 |
| C.经过t/2,它的瞬时速度是x/t | D.经过x/2,它的瞬时速度是 |