下列四个命题:①一组对边平行,另一组对边相等的四边形是等腰梯形;②对角线互相垂直且相等的四边形是正方形;③顺次连接菱形各边中点所得四边形是矩形;④等腰三角形腰上的高与中线重合。其中真命题有
| A.1个 | B.2个 | C.3个 | D.4个 |
以坐标原点 为圆心,作半径为2的圆,若直线 与 相交,则 的取值范围是
A. B. C. D.
如图,在距离铁轨200米的 处,观察由南宁开往百色的“和谐号”动车,当动车车头在 处时,恰好位于 处的北偏东 方向上;10秒钟后,动车车头到达 处,恰好位于 处的西北方向上,则这时段动车的平均速度是 米 秒.

A. B. C.200D.300
九年级(2)班同学根据兴趣分成五个小组,各小组人数分布如图所示,则在扇形图中,第一小组对应的圆心角度数是
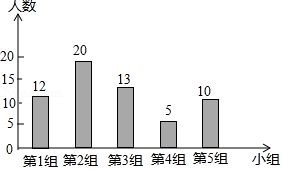
A. B. C. D.
观察以下一列数的特点:0,1, ,9, ,25, ,则第11个数是
A. B. C.100D.121
如图所示的正三棱柱,它的主视图、俯视图、左视图的顺序是
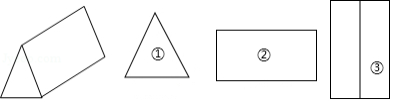
A.①②③B.②①③C.③①②D.①③②