小明所在班组织全部同学参加上海世博园，由于时间原因，每个学生只能在所给的场馆单（如图）上随机选择，选择方式规定为在3个发展中国家馆和4个发达国家馆中分别选一个馆参观。场馆单上的3个发展中国家馆包括：A中国馆、B印度馆、C巴西馆；4个发达国家馆包括：D美国馆、E日本馆、F德国馆、G法国馆，其中中国馆、印度馆、日本馆属于亚洲馆。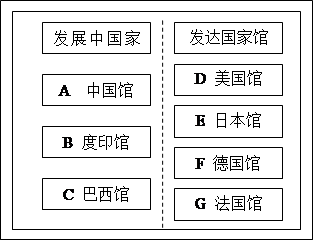
（1）请你用列表或画树状图的方法，分析并写出小明所有可能的参观方式。（馆名用字母表示即可）
（2）求小明所选择参观的两个馆恰好都是亚洲馆的概率。
如图，抛物线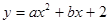
与x轴交于点A（1，0）和B（4，0）．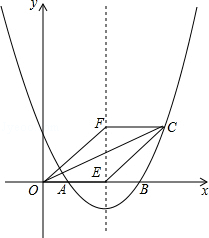
（1）求抛物线的解析式；
（2）若抛物线的对称轴交x轴于点E，点F是位于x轴上方对称轴上一点，FC∥x轴，与对称轴右侧的抛物线交于点C，且四边形OECF是平行四边形，求点C的坐标；
（3）在（2）的条件下，抛物线的对称轴上是否存在点P，使△OCP是直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．
将一副三角尺（在Rt△ABC中，∠ACB=90°，∠B=60°；在Rt△DEF中，∠EDF=90°，∠E=45°）按如图①摆放，点D为AB的中点，DE交AC于点P，DF经过点C．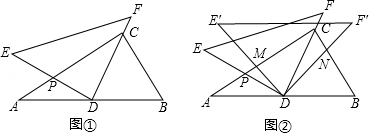
（1）求∠ADE的度数；
（2）将△DEF绕点D顺时针方向旋转角α（0°＜α＜60°），此时的等腰直角三角尺记为△DE′F′，DE′交AC于点M，DF′交BC于点N，如图②，试判断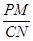
的值是否随着α的变化而变化？如果不变，请求出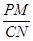的值；如果变化，请说明理由．
目前节能灯在城市已基本普及，今年某省面向县级及农村地区推广，为响应号召，某商场计划购进甲、乙两种型号节能灯共1200只，这两种型号节能灯的进货价、销售价如下表：
| 进货价（元/只） |
销售价（元/只） |
|
| 甲型 |
25 |
30 |
| 乙型 |
45 |
60 |
（1）问购进甲、乙两种节能灯各多少只，进货款恰好为46000元？
（2）如果商场在销售完节能灯时所获利润不超过进货款的30%情况下，如何进货才能使该商场销售完节能灯所获利润最大，最大利润是多少元？
如图，已知⊙O的直径为AB，AC⊥AB于点A，BC与⊙O相交于点D，连接AD．在AC上取一点E，使得ED=EA．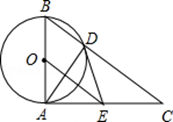
（1）求证：ED是⊙O的切线；
（2）当OA=3，AE=4时，求BC的长度．
如图，四边形ABCD是矩形，把矩形沿对角线AC折叠，点B落在点E处，CE与AD相交于点O．
（1）求证：△AOE≌△COD；
（2）若∠OCD=30°，AB=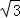
，求△AOC的面积．