设 ,且
,且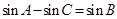 ,
, ,则
,则 等于( )
等于( )
A.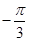 |
B. |
C. |
D. 或 或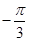 |
已知函数 的导函数为偶函数,则
的导函数为偶函数,则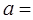 ()
()
| A.0 | B.1 | C.2 | D.3 |
在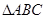 中,若
中,若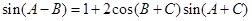 ,则
,则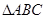 的形状一定是
的形状一定是
| A.等边三角形 | B.不含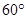 角的等腰三角形 角的等腰三角形 |
| C.钝角三角形 | D.直角三角形 |
已知函数 的定义域为
的定义域为 的值域为
的值域为 ,则
,则 ()
()
A. |
B. |
C. |
D. |
在平面直角坐标系中,定义 为两点
为两点 ,
, 之间的“折线距离”.在这个定义下,给出下列命题:
之间的“折线距离”.在这个定义下,给出下列命题:
①到原点的“折线距离”等于 的点的集合是一个正方形;
的点的集合是一个正方形;
②到原点的“折线距离”等于 的点的集合是一个圆;
的点的集合是一个圆;
③到 两点的“折线距离”相等的点的轨迹方程是
两点的“折线距离”相等的点的轨迹方程是 ;
;
④到 两点的“折线距离”差的绝对值为
两点的“折线距离”差的绝对值为 的点的集合是两条平行线.其中正确的命题有()
的点的集合是两条平行线.其中正确的命题有()
| A.1个 | B.2 个 | C.3 个 | D.4个 |
两条平行直线和圆的位置关系定义为:若两条平行直线和圆有四个不同的公共点,则称两条平行线和圆“相交”;若两平行直线和圆没有公共点,则称两条平行线和圆“相离”;若两平行直线和圆有一个、两个或三个不同的公共点,则称两条平行线和圆“相切”.已知直线 相切,则a的取值范围是()
相切,则a的取值范围是()
A. |
B. |
C.-3≤a≤一 或 或 ≤a≤7 ≤a≤7 |
D.a≥7或a≤—3 |