如图,在直角坐标系中,点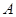 是反比例函数
是反比例函数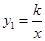 的图象上一点,
的图象上一点, 轴的正半轴于
轴的正半轴于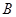 点,
点,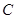 是
是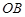 的中点;一次函数
的中点;一次函数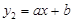 的图象经过
的图象经过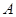 、
、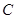 两点,并交
两点,并交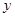 轴于点
轴于点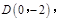 若
若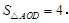
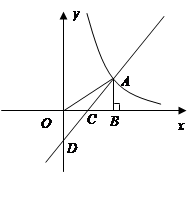
(1)求反比例函数和一次函数的解析式;
(2)观察图象,请写出在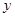 轴的右侧,当
轴的右侧,当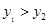 时,
时,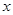 的取值范围.
的取值范围.
计算
(1)解不等式:5(x﹣2)﹣2(x+1)>3.
(2)解不等式 ≤
≤ ,并求出它的非负整数解。
,并求出它的非负整数解。
已知△ABC,利用直尺和圆规,根据下列要求作图(保留作图痕迹,不要求写作法).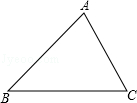
(1)作∠ABC的平分线BD交AC于点D;
(2)作线段BD的垂直平分线交AB于点E,交BC于点F.
寻找公式,求代数式的值:从2开始,连续的偶数相加,它们的和的情况如下表:
(1)当n个最小的连续正偶数相加时,它们的和S与n之间的关系,用公式表示为_________________;
(2)并按此规律计算: ①2+4+6+…+300的值;②162+164+166+…+400的值.
如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.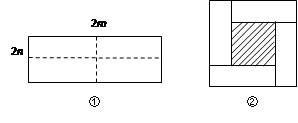
(1)你认为图②中的阴影部分的正方形的边长等于 .
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积,
方法① .方法② .
(3)观察图②,你能写出(m+n)2,(m-n)2,mn这三个代数式之间的等量关系吗?
(4)根据(3)题中的等量关系,解决如下问题:若a+b=6,ab=4,则求(a-b)2的值.
为庆祝我国首个空间实验室“天宫一号”顺利升空,学校开展了火箭模型制作比赛,如图为火箭模型的截面图,下面是梯形,中间是长方形,上面是三角形.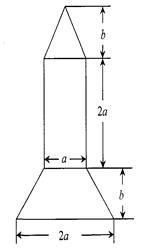
(1) 用a、b的代数式表示该截面的面积S;
(2) 当a=2cm,b=3cm时,求这个截面的面积.