在平面直角坐标系中，O是坐标原点，直角梯形AOCD的顶点A的坐标为
（0，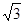
），点D的坐标为（1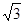，），点C在
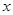轴的正半轴上，过点O且以点D为顶点的抛物线经过点C，点P为CD的中点．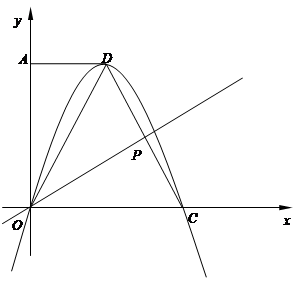
（1）求抛物线的解析式及点P的坐标；
（2） 在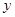
轴右侧的抛物线上是否存在点Q，使以Q为圆心的圆同时与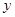轴、直线OP相切．若存在，请求出满足条件的点Q的坐标；若不存在，请说明理由；
（3）点M为线段OP上一动点（不与O点重合），过点O、M、D的圆与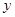轴的正半轴交于点N．求证：OM+ON为定值．
（4）在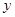轴上找一点H，使∠PHD最大．试求出点H的坐标．
解方程：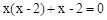
（本题12分）如图，点O是等边△ABC内一点，D是△ABC外的一点， ∠AOB= 110°，
∠BOC=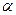 
，△BOC ≌△ADC，∠OCD＝60°，连接OD。
（1）求证：△OCD是等边三角形；
（2）当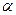＝150°时，试判断△AOD 的形状，并说明理由；
（3）探究：当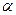为多少度时，△AOD是等腰三角形。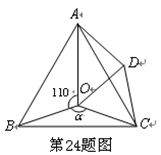
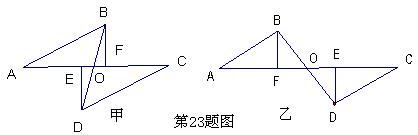
（本题10分）如图甲，已知A、E、F、C在一条直线上，AE=CF，过E、F分别作DE⊥AC，
BF⊥AC，且AB=CD。
（1）试问OE=0F吗？请说明理由。
（2）若△DEC沿AC方向平移到如图乙的位置，其余条件不变，上述结论是否仍成立？请说明理由。
 |
（本题10分）如图所示的一块地，∠ADC=90°，AD=3m，CD=4m，AB=13m，BC=12m，求这块地的面积。
 |
（本题8分）如图，△ABC中，AB=AC，D为BC边的中点，F为CA的延长线上一点，过点F 作FG⊥BC于G点，并交AB于E点，试说明下列结论成立的理由：
（1）AD∥FG；
（2）△AEF是等腰
三角形