如图,水平地面上有一转台,高h=10米,由半径为R=1米和r=0.5米的两个半圆柱拼合而成,可绕其中心轴转动,平台边缘上放有两个质量均为m=0.1kg的物体,可视为质点,由一根长为1.5m的细线连接在一起,且细线过转台的圆心,A、B两物体与平台接触面的动摩擦系数均为μ=0.2,最大静摩擦力等于滑动摩擦力。现在使转台转动的角速度缓慢地增大,g=10m/s2,求:
(1)在绳子无张力时,ω的最大值为多少?
(2)在A、B两个物体不滑动时,ω的最大值又为多少?
(3)接第2小题,当ω取最大值时,绳子突然断裂, A、B两个物体将同时离开转台,当两个物体同时第一次着地时,其着地点距离是多少?(结果带上根号)
某科研单位设计了一空间飞行器,飞行器从地面起飞时,发动机提供的动力方向与水平方向夹角α=60°,使飞行器恰恰与水平方向成θ=30°角的直线斜向右上方匀加速飞行,经时间t后,将动力的方向沿逆时针旋转60°同时适当调节其大小,使飞行器依然可以沿原方向匀减速飞行,飞行器所受空气阻力不计,求: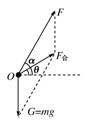
(1)t时刻飞行器的速率;
(2)整个过程中飞行器离地的最大高度.
一质量m=0.5 kg的滑块以一定的初速度冲上一倾角为30°足够长的斜面,某同学利用DIS实验系统测出了滑块冲上斜面过程中多个时刻的瞬时速度,如图所示为通过计算机绘制出的滑块上滑过程的v-t图象(g取10 m/s2).求: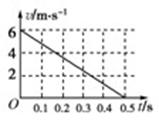
(1)滑块冲上斜面过程中加速度的大小;
(2)滑块与斜面间的动摩擦因数;
(3)判断滑块最后能否返回斜面底端.若能返回,求出滑块返回斜面底端时的动能;若不能返回,求出滑块所停位置.
如图所示,AB为半径R=0.8 m的1/4光滑圆弧轨道,下端B恰与小车右端平滑对接.小车质量M=3 kg,车长L=2.06 m,车上表面距地面的高度h=0.2 m.现有一质量m=1 kg的滑块,由轨道顶端无初速释放,滑到B端后冲上小车.已知地面光滑,滑块与小车上表面间的动摩擦因数μ=0.3,当车运行了1.5 s时,车被地面装置锁定.(g=10 m/s2)试求:
(1)滑块刚到达B端瞬间,轨道对它支持力的大小;
(2)车被锁定时,车右端距轨道B端的距离;
(3)从车开始运动到被锁定的过程中,滑块与车面间由于摩擦而产生的内能大小;
(4)滑块落地点离车左端的水平距离.
如图,质量m=2kg的物体静止于水平地面的A处,A、B间距L=20m。用大小为30N,沿水平方向的外力拉此物体,经t0=2s拉至B处。(sin37º=0.6,cos37º=0.8,g取10m/s2)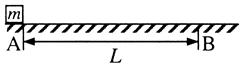
(1)求物体与地面间的动摩擦因数μ;
(2)用大小为30N,与水平方向成37°的力斜向上拉此物体,使物体从A处由静止开始运动并能到达B处,求该力作用的最短时间t。(答案可带根号)
一个宇航员在半径为R的星球上以初速度v0竖直上抛一物体,经t后物体落回宇航员手中.(1) 该星球表面重力加速度gx是多少?(2)为了使沿星球表面抛出的物体不再落回星球表面,抛出时的速度至少为多少?