已知万有引力常量G，某行星的半径R和绕该行星表面运行的卫星的周期T，可以求得下面哪些量：
| A．卫星的质量 | B．该行星表面的重力加速度 |
| C．该行星的同步卫星离其表面的高度 | D．该行星的第一宇宙速度 |
三个点电荷电场的电场线分布如图所示，图中a、b两点出的场强大小分别为
、
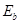，电势分别为
，则
| A．＞ |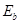
B．＜ |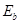
C． ＜ |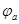
D．＞ |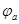
如图，在匀强磁场中固定放置一根串接一电阻R的直角形金属导轨aob（在纸面内），磁场方向垂直于纸面向里，另有两根金属导轨c、d分别平行于oa、ob放置。保持导轨之间接触良好，金属导轨的电阻不计。现经历以下四个过程：①以速率v移动d，使它与ob的距离增大一倍；②再以速率v移动c，使它与oa的距离减小一半；③然后，再以速率2v移动c，使它回到原处；④最后以速率2v移动d，使它也回到原处。设上述四个过程中通过电阻R的电量的大小依次为Q1、Q2、Q3和Q4，则( )
| A．Q1=Q2=Q3=Q4 | B．Q1=Q2=2Q3=2Q4 |
C．2Q1=2Q2=Q3=Q4 | D．Q1≠Q2＝Q3≠Q4 |
如图，为一理想变压器，K为单刀双掷开关，P为滑动变阻器的滑动触头，U1为加在原线圈两端的电压，I1为原线圈中的电流强度，则（）
| A．保持U1及P的位置不变，K由a合到b时，I1将增大 |
| B．保持U1及P的位置不变，K由b合到a时，R消耗的功率减小 |
| C．保持U1不变，K合在a处，使P上滑，I1将增大 |
| D．保持P的位置不变，K合在a处，若U1增大，I1将增大 |
如图所示，一个边长为a、电阻为R的等边三角形线框，在外力作用下，以速度v匀速穿过宽均为a的两个匀强磁场.这两个磁场的磁感应强度大小均为B方向相反.线框运动方向与底边平行且与磁场边缘垂直.取逆时针方向的电流为正.若从图示位置开始，线框中产生的感应电流I与沿运动方向的位移x之间的函数图象，下面四个图中正确的是（）
如图，平行导轨足够长，右端和电容相接，一根金属杆横放其上，以速度v匀速运动，不计摩擦和电阻。若突然把金属杆的速度减为零后，又立即释放，则此后滑线的运动情况是（）
| A．先向左作加速运动，再作向左的减速运动，直到最后停止 |
| B．先向左作加速运动，再作向左的匀速运动 |
| C．先向右作加速运动，再作向右的减速运动，直到最后停止 |
| D．先向右作加速运动，再作向右的匀速运动 |