如图所示，直角三角板ABC的两直角边AC、BC的长分别为40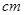
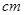和30，点G在斜边AB上，且BG＝30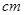，将这个三角板以G为中心按逆时针方向旋转90°至△A′B′C′的位置，那么旋转前后两个三角板重叠部分（四边形EFGD）的面积为 .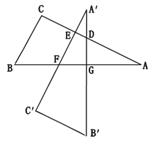 
在平面直角坐标系
中，我们把横 、纵坐标都是整数的点叫做整点．已知点
A（0，4），点B是
轴正半轴上的整点，记△AOB内部（不包括边界）的整点个数为m．当m=3时，点B的横坐标的所有可能值是 ▲；当点B的横坐标为4n（n为正整数）时，m=（用含n的代数式表示．）
如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的
位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上．已知纸板的两条直角边DE=40cm，EF=20cm，测得边DF离地面的高度AC="1.5" m，CD="8" m，则树高AB= ▲
．
若关于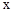
的方程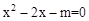
有两个相等的实数根，则
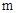的值是 ▲．
分解因式：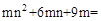
▲．
如图，P是矩形ABCD内的任意一点，连接PA、PB、PC、PD，得到△PAB、△PBC、△PCD、△PDA，设它们的面积分别是S1、S2、S3、S4，给出如下结论：
①S1+S2=S3+S4② S2+S4= S1+ S3
③若S3="2" S1，则S4="2" S2④若S1= S2，则P点在矩形的对角线上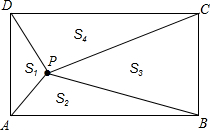
其中正确的结论的序号是 ▲（把所有正确结论的序号都填在横线上）.