今年4月20日，四川芦山发生了里氏7.0级大地震，给当地人民造成了巨大的损失，“一方有难，八方支援”，我县某中学全体师生积极捐款，其中九年级的三个班学生的捐款金额如下表：
| 班级 |
（1）班 |
（2）班 |
（3）班 |
| 金额（元） |
2000 |
 |
吴老师统计时不小心把墨水滴到了其中两个班级的捐款金额上，但他知道下面三条信息：信息一：这三个班的捐款总金额是7700元；信息二：（2）班的捐款金额比（3）班的捐款金额多300元；信息三：（1）班学生平均每人捐款的金额大于48元，小于51元．请根据以上信息，帮助吴老师解决下列问题：
（1）求出（2）班与（3）班的捐款金额各是多少元；
（2）求出（1）班的学生人数．
化简：
如图，∠MON=90°，A、B分别是OM、ON上的点，OB=4．点C是线段AB的中点，将线段AC以点A为旋转中心，沿顺时针方向旋转90°，得到线段AD，过点B作ON的垂线
．
（1）当点D恰好落在垂线上时，求OA的长；
（2）过点D作DE⊥OM于点E，将（1）问中的△AOB以每秒2个单位的速度沿射线OM方向平移，记平移中的△AOB为△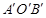
，当点O′与点E重合时停止平移．设平移的时间为t秒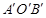，△与△DAE重叠部分的面积为S，请直接写出S与t之间的函数关系式以及自变量t的取值范围；
（3）在（2）问的平移过程中，若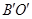
与线段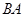
交于点P，连接
，
，
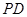，是否存在这样的t，使△
是等腰三角形？若存在，求出t的值；若不存在，请说明理由．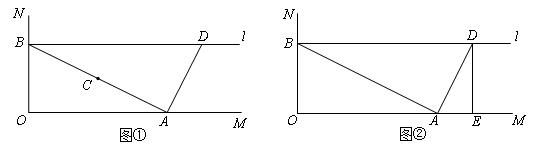
如图，在平面直角坐标系中，二次函数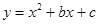
的图象与x轴交于A、B两点， A点在原点的左侧，B点的坐标为（
，
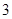），与y轴交于C（，
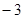）点，点P是直线BC下方的抛物线上一动点．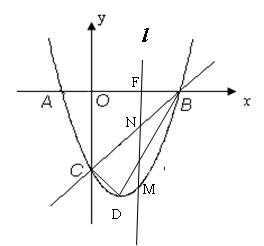
（1）求这个二次函数的解析式；
（2）若抛物线的顶点为点D，求△BCD的面积；
（3）设M是（1）所得抛物线上第四象限内的一个动点，过点M作直线l⊥x 轴于点F，交直线BC于点N。试问：线段MN的长度是否存在最大值？若存在，求出它最大值及此时M点的坐标；若不存在，请说明理由．
已知，如图，在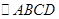
中，AE⊥BC，垂足为E，点F为CE上的一点，点G为CD上的一点，CF=CG，连接DF、EG、AG， AG=EG，∠1=∠2．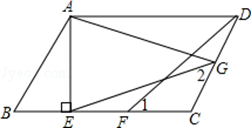
（1）若CE=4，AE=3，求BE的长；
（2）求证：∠CEG=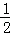
∠AGE．
某蔬菜店第一次用800元购进某种蔬菜，由于销售状况良好，该店又用了1400元第二次购进该种蔬菜，所购数量是第一次购进数量的2倍，但进货价每千克少了0．5元。
（1）第一次所购的该蔬菜的进货价是每千克多少元？
（2）蔬菜店在销售中，如果两次售价均相同，并且忽略其他因素，要使该蔬菜店售完这些蔬菜获利不低于1700元，则该蔬菜每千克售价至少为多少？