如图，二次函数
的图象与
轴交于B、C两点（点B在点C的左侧），一次函数
的图象经过点B和二次函数图象上另一点A. 点A的坐标（4 ，3），
.
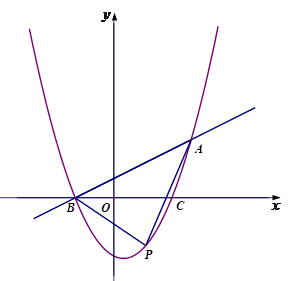
（1）求二次函数和一次函数解析式；
（2）若点P在第四象限内，求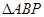
面积S的最大值并求出此时点P的坐标；
（3）若点M在直线AB上，且与点A的距离是到轴距离的
倍，求点M的坐标.
解方程
（1）4x﹣3（5﹣x）=6
（2）
﹣
=1．
如图，线段AB=8cm，C是AB的中点，点D在CB上，DB=
CB，则线段CD长是 ．
为庆祝第29届北京奥运圣火在泉州站传递，甲、乙两校联合准备文艺汇演．甲、乙两校共92人（其中甲校人数多于乙校人数，且甲校人数不够90人）准备统一购买服装（一人买一套）参加演出，下面是服装厂给出的演出服装的价格表：
| 购买服装的套数 |
1套至45套 |
46套至90套 |
91套及以上 |
| 每套服装的价格 |
60元 |
50元 |
40元 |
如果两所学校分别单独购买服装，一共应付5000元．
（1）如果甲、乙两校联合起来购买服装，那么比各自购买服装共可以节省多少钱？
（2）甲、乙两校各有多少学生准备参加演出？
（3）如果甲校有9名同学抽调去参加迎奥运书法比赛不能参加演出，那么你有几种购买方案，通过比较，你该如何购买服装才能最省钱？
甲、乙两个旅行团同时去苏州旅游，已知乙团人数比甲团人数多4人，两团人数之和恰等于两团人数之差的18倍．
（1）问甲、乙两个旅行团的人数各是多少？
（2）若乙团中儿童人数恰为甲团人数的3倍少2人，某景点成人票价为每张100元，儿童票价是成人票价的六折，两旅行团在此景点所花费的门票费用相同，求甲、乙两团儿童人数各是多少？
在直线AB上，点P在A、B两点之间，点M为线段PB的中点，点N为线段AP的中点，若AB=m，且使关于x的方程mx+4=2（x+m）有无数个解．
（1）求线段AB的长；
（2）试说明线段MN的长与点P在线段AB上的位置无关；
（3）若点C为线段AB的中点，点P在线段CB的延长线上，试说明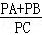
的值不变．