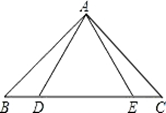
如图,已知抛物线y=ax2+2x+c的顶点为A(―1,―4),与y轴交于点B,与x轴负半轴交于点C.
(1)求这条抛物线的函数关系式;
(2)点P为第三象限内抛物线上的一动点,连接BC、PC、PB,求△BCP面积的最大值,并求出此时点P的坐标;
(3)点E为抛物线上的一点,点F为x轴上的一点,若四边形ABEF为平行四边形,请直接写出所有符合条件的点E的坐标.
-0.5-(-3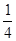 )+2.75-(+7
)+2.75-(+7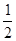 )
)
如图1,OP是∠MON的平分线,请你利用刻度尺在该图形上画一对以OP所在直线为对称轴的全等三角形,并将添加的全等条件标注在图上.
请你参考这个作全等三角形的方法,解答下列问题: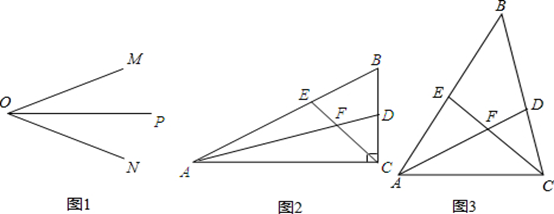
(1)如图2,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC和∠BCA的平分线,AD、CE相交于点F,求∠EFA的度数;
(2)在(1)的条件下,请判断FE与FD之间的数量关系,并说明理由;
(3)如图3,在△ABC中,如果∠ACB不是直角,而( 1 )中的其他条件不变,试问在(2)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
如图,点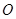 是等边
是等边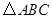 内一点,
内一点,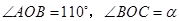 .将
.将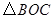 绕点
绕点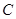 按顺时针方向旋转
按顺时针方向旋转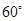 得
得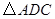 ,连接
,连接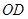 .
.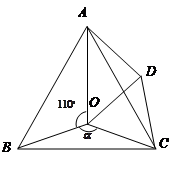
(1)求证: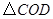 是等边三角形;
是等边三角形;
(2)当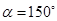 时,试判断
时,试判断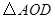 的形状,并说明理由;
的形状,并说明理由;
(3)探究:当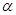 为多少度时,
为多少度时,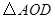 是等腰三角形?
是等腰三角形?
如图,在四边形ABCD中,∠ABC=∠ADC= 90º,M、N分别是AC、BD的中点,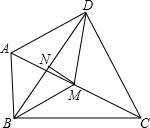
求证:(1)MD=MB;
(2)MN平分∠DMB.
如图,已知AB=AC,AD=AE.求证:BD=CE.