标有-3,-2,4的三张不透明的卡片,除正面写有不同的数字外,其余的值都相同,将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记为一次函数解析式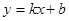 的k值,第二次从余下的两张卡片中再抽取一张,上面标有的数字记为一次函数解析式的b值。
的k值,第二次从余下的两张卡片中再抽取一张,上面标有的数字记为一次函数解析式的b值。
(1)写出k为负数的概率;
(2)求一次函数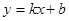 的图象不经过第一象限的概率。(用树状图或列举法求解)
的图象不经过第一象限的概率。(用树状图或列举法求解)
如图,矩形OABC的顶点A、C分别在x轴和y轴上,点 的坐标为(2,3).双曲线
的坐标为(2,3).双曲线 的图像经过BC的中点D,且与AB交于点E,连接DE.
的图像经过BC的中点D,且与AB交于点E,连接DE.
(1)求k的值及点E的坐标;
(2)若点F是边上一点,且ΔFCB∽ΔDBE,求直线FB的解析式
某省为解决农村饮用水问题,省财政部门共投资10亿元对各市的农村饮用水的“改水工程”予以一定比例的补助.2012年,A市在省财政补助的基础上投入600万元用于“改水工程”,计划以后每年以相同的增长率投资,2014年该市计划投资“改水工程”864万元.
(1)求A市投资“改水工程”的年平均增长率;
(2)从2012年到2014年,A市三年共投资“改水工程”多少万元?
先化简,再求值: ,其中
,其中 是方程
是方程 的根.
的根.
如图14-1,在锐角△ABC中,AB = 5,AC =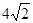 ,∠ACB = 45°.
,∠ACB = 45°.
计算:求BC的长;
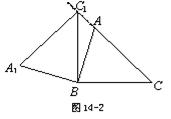
操作:将图14-1中的△ABC绕点B按逆时针方向旋转,得到△A1BC1.如图14-2,当点C1在线段CA的延长线上时.
(1)证明:A1C1⊥CC1;
(2)求四边形A1BCC1的面积;

探究:
将图14-1中的△ABC绕点B按逆时针方向旋转,得到△A1BC1.连结AA1,CC1,如图14-3.若△ABA1的面积为5,求点C到BC1的距离;
拓展:
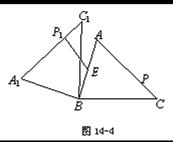
将图14-1中的△ABC绕点B按逆时针方向旋转,得到△A1BC1.点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,如图14-4.
(1)若点P是线段AC的中点,求线段EP1长度的最大值与最小值;
(2)若点P是线段AC上的任一点,直接写出线段EP1长度的最大值与最小值.
小明家今年种植樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行了跟踪记录,并将记录情况绘成图表.日销售量y(单位:kg)与上市时间x(单位:天)的函数关系如图13所示,樱桃单价w(单位:元/ kg)与上市时间x(单位:天)的函数关系列表所示,第1天到第a天的单价相同,第a天之后,单价下降,w与x之间是一次函数关系.
樱桃单价w与上市时间x的关系
| x(天) |
1 |
a |
9 |
11 |
13 |
… |
| w(元/kg) |
32 |
32 |
24 |
20 |
16 |
… |
请解答下列问题:
(1)观察图象,直接写出日销售量的最大值;
(2)求小明家樱桃的日销售量y与上市时间x的函数解析式;
(3)求a的值;
(4)第12天的销售金额是最多的吗?请说明你的观点和依据.