某地为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地决策,自来水公司随机抽取部分用户的用适量数据,并绘制了如下不完整统计图(每组数据包括右端点但不包括左端点),请你根据统计图解决下列问题: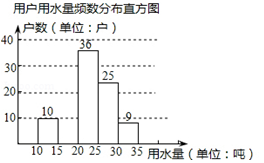

(1)此次调查抽取了多少用户的用水量数据?
(2)补全频数分别直方图,求扇形统计图中“25吨~30吨”部分的圆心角度数;
(3)如果自来水公司将基本用水量定为每户25吨,那么该地20万用户中约有多少用户的用水全部享受基本价格?
已知:如图,AC⊙O是的直径,BC是⊙O的弦,点P是⊙O外一点,∠PBA=∠C.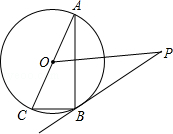
(1)求证:PB是⊙O的切线;
(2)若OP∥BC,且OP=8,BC=2.求⊙O的半径.
某校七年级准备购买一批笔记本奖励优秀学生,在购买时发现,每本笔记本可以打九折,用360元钱购买的笔记本,打折后购买的数量比打折前多10本.
(1)求打折前每本笔记本的售价是多少元?
(2)由于考虑学生的需求不同,学校决定购买笔记本和笔袋共90件,笔袋每个原售价为6元,两种物品都打九折,若购买总金额不低于360元,且不超过365元,问有哪几种购买方案?
如图,为了缓解交通拥堵,方便行人,在某街道计划修建一座横断面为梯形ABCD的过街天桥,若天桥斜坡AB的坡角∠BAD为35°,斜坡CD的坡度为i=1:1.2(垂直高度CE与水平宽度DE的比),上底BC=10m,天桥高度CE=5m,求天桥下底AD的长度?(结果精确到0.1m,参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
有三张正面分别标有数字:﹣1,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
(1)请用列表或画树形图的方法(只选其中一种),表示两次抽出卡片上的数字的所有结果;
(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点(x,y)落在双曲线上 上的概率.
上的概率.
2013年6月6日第一届南亚博览会在昆明举行.某校对七年级学生开展了“南博会知多少?”的调查活动,采取随机抽样的方法进行问卷调查,问卷调查的结果分为“不太了解”、“基本了解”、“比较了解”、“非常了解”四个等级,对调查结果进行统计后,绘制了如下不完整的条形统计图:
根据以上统计图提供的信息,回答下列问题:
(1)若“基本了解”的人数占抽样调查人数的25%,此次调查抽取了 学生;
(2)补全条形统计图;
(3)若该校七年级有600名学生,请估计“比较了解”和“非常了解”的学生共有多少人?