已知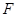
是双曲线
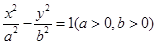的左焦点，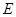
是双曲线的右顶点，过点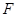且垂直于
轴的直线与双曲线交于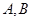
两点，若
是锐角三角形，则该双曲线的离心率
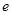的取值范围为（ ）
A． |
B． |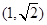
C． |
D． |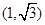
如果a<0,b<0,则必有( )
| A．a3+b3≥ab2+a2b | B．a3+b3≤ab2+a2b |
| C．a3+b3>ab2+a2b | D．a3+b3<ab2+a2b |
要证明a2+b2-1-a2b2≤0,只要证明( )
| A．2ab-1-a2b2≤0 | B．a2+b2-1- ≤0 |
C． -1-a2b2≤0 |
D．(a2-1)(b2-1)≥0 |
在证明命题“对于任意角θ,cos4θ-sin4θ=cos2θ”的过程:“cos4θ-sin4θ=(cos2θ+sin2θ)·(cos2θ-sin2θ)=cos2θ-sin2θ=cos2θ”中应用了( )
| A．分析法 |
| B．综合法 |
| C．分析法和综合法综合使用 |
| D．间接证法 |
若在曲线f(x,y)=0上存在两个不同点处的切线重合,则称这条切线为曲线f(x,y)=0的“自公切线”.下列方程:①x2-y2=1;②y=x2-|x|;③y=3sinx+4cosx;④|x|+1=
对应的曲线中存在“自公切线”的有( )
| A．①② | B．②③ |
| C．①④ | D．③④ |
在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点,如果函数f(x)的图象恰好通过n(n∈N*)个整点,则称函数f(x)为n阶整点函数.有下列函数:
①f(x)=x+
(x>0);②g(x)=x3;
③h(x)=(
)x;④φ()=lnx.
其中是一阶整点函数的是( )
| A．①②③④ | B．①③④ |
| C．④ | D．①④ |