2012年秋冬北方干旱,光明社区出现饮用水紧张,每天需从社区外调运饮用水120吨.现从甲、乙两水厂调运饮用水到社区供水点,甲厂每天最多可调出80吨,乙厂每天最多可调出90吨.从两水厂运水到光明社区供水点的路程和运费如下表:
| |
到光明社区供水点的路程(千米) |
运费(元/吨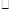 千米) 千米) |
| 甲厂 |
20 |
12 |
| 乙厂 |
14 |
15 |
(1)若某天调运水的总运费为26700元,则从甲、乙两水厂各调运了多少吨饮用水?
(2)设某天从甲厂调运饮用水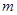 吨,总运费为
吨,总运费为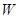 元,试写出
元,试写出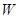 关于
关于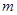 的函数关系式,并求出这天运费最少为多少元?
的函数关系式,并求出这天运费最少为多少元?