用反证法证明命题“三角形三个内角至少有一个不大于60o”时，应假设（）
| A．三个内角都不大于60o |
| B．三个内角至多有一个大于60o |
| C．三个内角都大于60o |
| D．三个内角至多有两个大于60o |
在复平面内，复数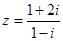
（i是虚数单位）对应的点在（）
| A．第一象限 | B．第二象限 | C．第三象限 | D．第四象限 |
若
为奇函数，且
是
的一个零点，则
一定是下列哪个函数的零点 （）
A． |
B． |
C． |
D． |
一个袋中装有大小相同的5个白球和3个红球，现在不放回的取2次球，每次取出一个球，记“第1次拿出的是白球”为事件
，“第2次拿出的是白球”为事件
，则事件与同时发生的概率是（）
A． |
B． |
C． |
D． |
若随机变量
的分布列如表:则
（）
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
 |
A．
B．
C．
D．
，
，A为动点，
，则
与
夹角的最小值为（ ）
