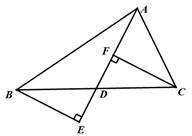
如图，△ABC和△DEF是两个全等的等腰直角三角形，∠BAC=∠EDF=90°，△DEF的顶点E与△ABC的斜边BC的中点重合．将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q．
（1）如图①，当点Q在线段AC上，且AP=AQ时，求证：△BPE≌△CQE；
（2）如图②，当点Q在线段CA的延长线上时，求证：△BPE∽△CEQ；并求当BP=
，CQ=
时，P、Q两点间的距离 (用含的代数式表示)．
如果将抛物线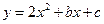
沿直角坐标平面先向左平移3个单位，再向下平移2个单位，得到了抛物线
．
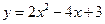（1）试确定b，c的值；
（2）求出抛物线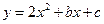的对称轴和顶点坐标.
如图，在△ABC中，AD是BC边的中线，过点C、B分别作AD及其延长线的垂线CF、BE，垂足分别为点F、E．求证：BE=CF
解不等式
，并将解集在数轴上表示出来．
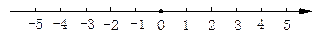
如图，直角梯形ABCD中，AD∥BC，∠ABC＝90°，已知AD＝AB＝3，BC＝4，动点P从B点出发，沿线段BC向点C作匀速运动；动点Q从点D 出发，沿线段DA向点A作匀速运动．过Q点垂直于AD的射线交AC于点M，交BC于点N．P、Q两点同时出发，速度都为每秒1个单位长度．当Q点运动到A点，P、Q两点同时停止运动．设点Q运动的时间为t秒．
(1) 求NC，MC的长(用t的代数式表示)；
(2) 当t为何值时，四边形PCDQ构成平行四边形？
(3) 当t为何值时,射线QN恰好将△ABC的面积平分？
并判断此时△AB
C的周长是否也被射线QN平分.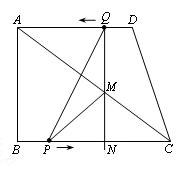
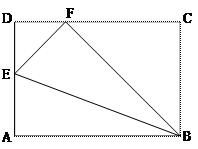
如图，已知一矩形ABCD，若把△ABE沿折痕BE向上翻折，A点恰好落在DC上，设此点为F，且这时AE:ED=5:3，BE=5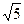
，这个矩形的长宽各是多少？