甲布袋中有三个红球,分别标有数字1,2,3;乙布袋中有三个白球,分别标有数字2,3,4.这些球除颜色和数字外完全相同.小亮从甲袋中随机摸出一个红球,小刚从乙袋中随机摸出一个白球.
(1)用画树状图(树形图)或列表的方法,求摸出的两个球上的数字之和为6的概率;
(2)小亮和小刚做游戏,规则是:若摸出的两个球上的数字之和为奇数,小亮胜;否则,小刚胜.你认为这个游戏公平吗?为什么?
如图,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD。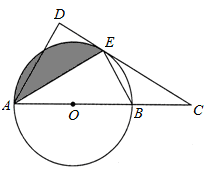
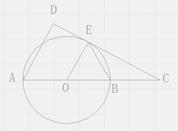
(1)求证:AE平分∠DAC;
(2)若AB=6,∠ABE=60°,①求AD的长;②求出图中阴影部分的面积。
小明是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,A、B、D在同一直线上,EF∥AD,∠CAB=∠EDF=90°,∠C=45°,∠E=60°,量得DE=8
(1)EF=,∠DFB= 度
(2)请求出BD的长。
据了解,今年中考我市某高中有招收艺术特色班,为了解学生的艺术特长发展情况,某校初三年段决定围绕“在舞蹈、乐器、声乐、戏曲、其它活动项目中,你最喜欢哪一项活动(每人只限一项)”的问题,在全年段随机抽取部分学生进行问卷调查,并将调查结果绘制成如下两幅不完整的统计图.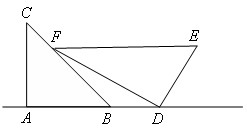

请你根据统计图解答下列问题:
(1)在这次调查中一共抽查了名学生,其中,喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为,喜欢“戏曲”活动项目的人数是人;
(2)若在“舞蹈、乐器、声乐、戏曲”活动项目任选两项设立课外兴趣小组,请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项活动的概率.
(1)如图,点A.B.D.E在同一直线上,AD=EB,BC∥DF,
∠C=∠F.求证:BC=DF.
(2) 雅安地震灾情牵动全国人民的心.某厂计划加工1500顶帐篷支援灾区,由于紧急救灾需要,工厂将工作效率提高到原计划的2倍,结果提前5天完成了任务.求原计划每天加工多少顶帐篷.
(1) 计算:(3-π)0+|―2013|-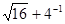
(2) 已知3a2+a=2,求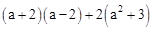 +a的值.
+a的值.